题目内容
4.已知向量$\overrightarrow b,\overrightarrow c$在正方形网格中的位置如图所示,则$\overrightarrow b+\overrightarrow c$=(2,-2)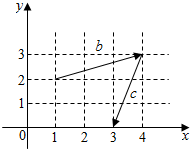
分析 根据图形,求出向量$\overrightarrow{b}$、$\overrightarrow{c}$的坐标表示,再求出$\overrightarrow b+\overrightarrow c$的坐标表示.
解答 解:根据题意,向量$\overrightarrow{b}$=(4-1,3-2)=(3,1),
$\overrightarrow{c}$=(3-4,0-3)=(-1,-3),
∴$\overrightarrow b+\overrightarrow c$=(3-1,1-3)=(2,-2).
故答案为(2,-2).
点评 本题考查了平面向量的坐标表示与运算问题,是基础题目.

练习册系列答案
相关题目
18.设i为虚数单位,a,b∈R,下列命题中:
①(a+1)i是纯虚数;
②若a>b,则a+i>b+i;
③若(a2-1)+(a2+3a+2)i是纯虚数,则实数a=±1;
④2i2>3i2.其中,真命题的个数有( )
①(a+1)i是纯虚数;
②若a>b,则a+i>b+i;
③若(a2-1)+(a2+3a+2)i是纯虚数,则实数a=±1;
④2i2>3i2.其中,真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.下列判断错误的是( )
| A. | “am2<bm2”是“a<b”的充分不必要条件 | |
| B. | 命题“x∈R,x3-x2-1≤0”的否定是“?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$-1>0” | |
| C. | 若p,q均为假命题,则p∧q为假命题 | |
| D. | 函数y=1是幂函数 |
14.下列命题中为真命题的是( )
| A. | 若x≠0,则x+$\frac{1}{x}$≥2 | |
| B. | 若直线x-ay=0与直线x+ay=0互相垂直,则a=1 | |
| C. | 命题“若x2=1,则x=1或x=-1”的逆否命题为“若x≠1且x≠-1,则x2≠1” | |
| D. | 一个命题的否命题为真,则它的逆否命题一定为真 |
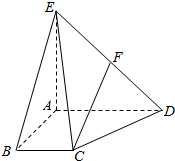 四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.
四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.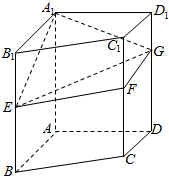 如图直四棱柱ABCD-A1B1C1D1,底面ABCD是直角梯形,AB∥DC,∠BAD=90°,AA1=AB=2CD=4,AD=2,E、F、G分别是侧棱BB1、C1C、DD1上的点,BE=2,DG=3.
如图直四棱柱ABCD-A1B1C1D1,底面ABCD是直角梯形,AB∥DC,∠BAD=90°,AA1=AB=2CD=4,AD=2,E、F、G分别是侧棱BB1、C1C、DD1上的点,BE=2,DG=3.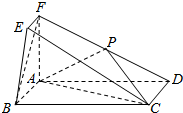 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P是棱DF的中点.