题目内容
11.对任意的实数k,直线y=kx+$\sqrt{3}$与圆x2+y2=4的位置关系一定是( )| A. | 相离 | B. | 相交但直线过圆心 | ||
| C. | 相切 | D. | 相交但直线不过圆心 |
分析 直线y=kx+$\sqrt{3}$过定点(0,$\sqrt{3}$),即可判断点与圆的位置关系.
解答 解:直线y=kx+2过定点A(0,$\sqrt{3}$),
∵AO=3<4,
∴点A在圆内,
即直线和圆相交,
∵(0,0)不在直线上,
∴直线不过圆心,
故选:D.
点评 本题主要考查直线和圆的位置关系的判断,根据直线过定点,判断点和圆的位置关系是解决本题的关键.

练习册系列答案
相关题目
13.设集合M={x|1<x<5},N={0,2,3,5},则M∩N=( )
| A. | {x|2<x<4} | B. | {0,2,3} | C. | {2,3} | D. | {x|2<x<3} |
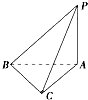
 如图所示,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点. 已知∠BAC=$\frac{π}{2}$,AB=2,AC=2,PA=2.求:
如图所示,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点. 已知∠BAC=$\frac{π}{2}$,AB=2,AC=2,PA=2.求: