题目内容
已知数列{an}中，a1＝1，Sn是数列{an}的前n项和，且对任意n∈N*，有an＋1＝kSn＋1(k为常数)．
(1)当k＝2时，求a2、a3的值；
(2)试判断数列{an}是否为等比数列？请说明理由．
(1)当k＝2时，an＋1＝2Sn＋1，
令n＝1得a2＝2S1＋1，又a1＝S1＝1，得a2＝3；
令n＝2得a3＝2S2＋1＝2(a1＋a2)＋1＝9，∴a3＝9.
∴a2＝3，a3＝9.
(2)由an＋1＝kSn＋1，得an＝kSn－1＋1，
两式相减，得an＋1－an＝kan(n≥2)，
即an＋1＝(k＋1)an(n≥2)，
且
＝
＝k＋1，故an＋1＝(k＋1)an.
故当k＝－1时，an＝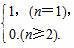
此时，{an}不是等比数列；
当k≠－1时，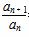
＝k＋1≠0，此时，{an}是首项为1，公比为k＋1的等比数列．
综上，当k＝－1时，{an}不是等比数列；
当k≠－1时，{an}是等比数列．
练习册系列答案
相关题目
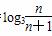(n∈N*)，设其前n项和为Sn，则使Sn<－4成立的最小自然数n等于( )
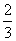)n－1 B．4×(
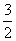)n D．4×(
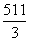，若从中去掉一项am，剩下的8项的平均值等于
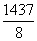，则m等于( )
)＋(a2－
)＋…＋(an－
)≥0成立的最大自然数是________．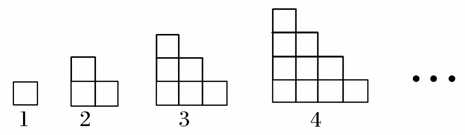
＋
，Q＝
，则( )