题目内容
18.已知函数f(x)=lnx+ax,g(x)=f(x)-ax+$\frac{a}{x-1}$.(1)若函数y=f(x)在x=1处取得极值,求实数a的值;
(2)若函数y=g(x)在(0,$\frac{1}{e}$)内有极值,求实数a的取值范围;
(3)在(2)的条件下,对任意t∈(1,+∞),s∈(0,1).求证:g(t)-g(s)>e-$\frac{1}{e}$+2.
分析 (1)求函数的导数,利用f′(1)=0,解方程即可.
(2)先化简函数g(x),根据函数y=g(x)在(0,$\frac{1}{e}$)内有极值,建立方程关系进行求解即可.
(3)根据g(x)的导数,判断函数g(x)的单调性,结合函数单调性和不等式之间的关系进行证明即可.
解答 解:(1)函数f(x)的定义域为(0,+∞),
则f′(x)=$\frac{1}{x}$+a,
若函数y=f(x)在x=1处取得极值,
则f′(1)=0,即1+a=0,
则a=-1
(2)g(x)=f(x)-ax+$\frac{a}{x-1}$=lnx+ax-ax+$\frac{a}{x-1}$=lnx+$\frac{a}{x-1}$.
∵函数g(x)=lnx+$\frac{a}{x-1}$在(0,$\frac{1}{e}$)内有极值
∴g′(x)=0在(0,$\frac{1}{e}$)内有解,令h(x)=x2-(a+2)x+1=(x-α)(x-β)
∵αβ=1,不妨设0<α<$\frac{1}{e}$,则β>e
∵h(0)=1>0,
∴h($\frac{1}{e}$)=$\frac{1}{{e}^{2}}$-$\frac{a+2}{e}$+1<0,
∴a>e+$\frac{1}{e}$-2;
(3)证明:由g′(x)>0,可得0<x<α或x>β;由g′(x)<0,可得α<x<1或1<x<β
∴g(x)在(0,α)内递增,在(α,1)内递减,在(1,β)内递减,在(β,+∞)递增
由s∈(0,1),可得g(s)≤g(α)=lnα+$\frac{a}{α-1}$,
由t∈(1,+∞),可得g(t)≥g(β)=lnβ+$\frac{a}{β-1}$,
∴g(t)-g(s)≥g(β)-g(α)
∵αβ=1,α+β=a+2
∴g(β)-g(α )=2lnβ+a×$\frac{α-β}{(β-1)(α-1)}$=2lnβ+a×$\frac{\frac{1}{β}-β}{2-(a+2)}$=2lnβ+β-$\frac{1}{β}$,
记h(β)=2lnβ+β-$\frac{1}{β}$(β>e)
则h′(β)=$\frac{2}{β}$+1+$\frac{1}{{β}^{2}}$>0,h(β)在(0,+∞)上单调递增
∴h(β)>h(e)=e+2-$\frac{1}{e}$,
∴g(t)-g(s)>e-$\frac{1}{e}$+2.
点评 本题以函数为载体,考查导数知识的运用,考查函数的极值与单调性,考查不等式的证明,综合性比较强.难度较大.

| A. | a+1 | B. | a+$\frac{3}{4}$ | C. | a2+1 | D. | $\frac{3}{4}$-a |
| A. | $({0,\frac{4}{27}})$ | B. | $({0,\frac{4}{27}}]$ | C. | $({\frac{4}{27},\frac{2}{3}})$ | D. | $({\frac{4}{27},\frac{2}{3}}]$ |
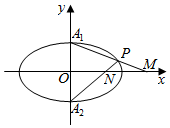 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F1(-$\sqrt{3}$,0),且过点E($\sqrt{3}$,$\frac{1}{2}$),设椭圆C的上下顶点分别为A1,A2,点P是椭圆上异于A1,A2的任一点,直线PA1,PA2分别交x轴于点M,N.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F1(-$\sqrt{3}$,0),且过点E($\sqrt{3}$,$\frac{1}{2}$),设椭圆C的上下顶点分别为A1,A2,点P是椭圆上异于A1,A2的任一点,直线PA1,PA2分别交x轴于点M,N.