题目内容
定义在R上的函数f（x），有如下四个命题：
①若f（0）=0，则函数f（x）是奇函数；
②若f（-4）≠f（4）则函数f（x）不是偶函数；
③若f（0）＜f（4），则函数f（x）是R上的增函数；
④若f（0）＜f（4），则函数f（x）不是R上的减函数．
其中正确的命题有 （写出你认为正确的所有命题的序号）．
①若f（0）=0，则函数f（x）是奇函数；
②若f（-4）≠f（4）则函数f（x）不是偶函数；
③若f（0）＜f（4），则函数f（x）是R上的增函数；
④若f（0）＜f（4），则函数f（x）不是R上的减函数．
其中正确的命题有
考点：函数奇偶性的判断,函数单调性的判断与证明
专题：计算题,函数的性质及应用
分析：比如y=x2+x，满足f（0）=0，不为奇函数，即可判断①；可从逆否命题考虑，即可判断②；
比如f（x）=x2+x，满足f（0）＜f（4），但f（x）在R上不为增函数，即可判断③；可从逆否命题考虑，即可判断④．
比如f（x）=x2+x，满足f（0）＜f（4），但f（x）在R上不为增函数，即可判断③；可从逆否命题考虑，即可判断④．
解答：
解：对于①，比如y=x2+x，满足f（0）=0，不为奇函数，故①错；
对于②，由于f（x）是偶函数，则f（-4）=f（4），故②对；
对于③，比如f（x）=x2+x，满足f（0）＜f（4），但f（x）在R上不为增函数，故③错；
对于④，由于函数f（x）是R上的减函数，则f（0）＞f（4），故④对．
故答案为：②④
对于②，由于f（x）是偶函数，则f（-4）=f（4），故②对；
对于③，比如f（x）=x2+x，满足f（0）＜f（4），但f（x）在R上不为增函数，故③错；
对于④，由于函数f（x）是R上的减函数，则f（0）＞f（4），故④对．
故答案为：②④
点评：本题考查函数的奇偶性和单调性的判断，考查运算能力，属于基础题和易错题．
练习册系列答案
相关题目
下列四个正方体图形中，A，B为正方体的两个顶点，M，N，P分别为其所在棱的中点，则能得出AB∥平面MNP的图形个数是（ ）
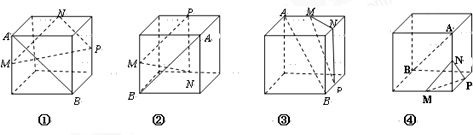
| A、1个 | B、2个 | C、3个 | D、4个 |
设正方体ABCD-A1B1C1D1的棱长为1，则平面B1AC被正方体内切球截得图形的面积（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知实数x，y满足x2+y2-4x+6y+4=0，则
的最小值是（ ）
|
A、2
| ||
B、
| ||
C、
| ||
D、
|