题目内容
17.过异于原点的点P(x0,y0)引椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的割线PAB,其中点A.B在椭圆上,点M是割线PAB上异于P的一点,且满足$\frac{AM}{MB}$=$\frac{AP}{PB}$.求证:点M在直线$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1上.
分析 设A(x1,y1),B(x2,y2),代入椭圆方程,设$\overrightarrow{AM}$=t$\overrightarrow{MB}$,$\overrightarrow{AP}$=-t$\overrightarrow{PB}$,M(x,y),运用向量的共线的坐标表示,计算
x0x,y0y,即可得证.
解答 证明:设A(x1,y1),B(x2,y2),
可得$\frac{{{x}_{1}}^{2}}{{a}^{2}}$+$\frac{{{y}_{1}}^{2}}{{b}^{2}}$=1,$\frac{{{x}_{2}}^{2}}{{a}^{2}}$+$\frac{{{y}_{2}}^{2}}{{b}^{2}}$=1,
设$\overrightarrow{AM}$=t$\overrightarrow{MB}$,$\overrightarrow{AP}$=-t$\overrightarrow{PB}$,M(x,y),
可得$\left\{\begin{array}{l}{x=\frac{{x}_{1}+t{x}_{2}}{1+t}}\\{y=\frac{{y}_{1}+t{y}_{2}}{1+t}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{0}=\frac{{x}_{1}-t{x}_{2}}{1-t}}\\{{y}_{0}=\frac{{y}_{1}-t{y}_{2}}{1-t}}\end{array}\right.$,
即有x0x=$\frac{{{x}_{1}}^{2}-{t}^{2}{{x}_{2}}^{2}}{1-{t}^{2}}$,y0y=$\frac{{{y}_{1}}^{2}-{t}^{2}{{y}_{2}}^{2}}{1-{t}^{2}}$,
则$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=$\frac{1}{1-{t}^{2}}$[($\frac{{{x}_{1}}^{2}}{{a}^{2}}$+$\frac{{{y}_{1}}^{2}}{{b}^{2}}$)-t2($\frac{{{x}_{2}}^{2}}{{a}^{2}}$+$\frac{{{y}_{2}}^{2}}{{b}^{2}}$)]
=$\frac{1}{1-{t}^{2}}$•(1-t2)=1.
点评 本题考查椭圆的方程和运用,考查向量的共线的坐标表示,以及化简整理的能力,属于中档题.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{3}$ |
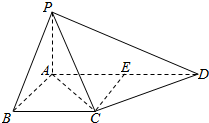 如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.