题目内容
8.某几何体的三视图如图所示,则该几何体的体积为( )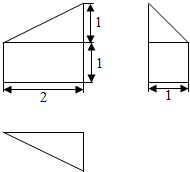
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{7}{3}$ |
分析 几何体为同底的三棱柱和三棱锥的组合体,代入体积公式计算即可求出体积.
解答 解:由三视图可知几何体为直三棱柱和三棱锥的组合体,直棱柱的底面为直角三角形,直角边为1,2,棱柱的高为1,三棱锥的底面与棱柱的底面相同,棱锥的高为1.
∴几何体的体积V=$\frac{1}{2}×1×2×1$+$\frac{1}{3}×\frac{1}{2}×1×2×1$=1+$\frac{1}{3}$=$\frac{4}{3}$.
故选B.
点评 本题考查了常见几何体的三视图和结构特征,体积计算,属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
3.已知一个几何的三视图如图所示,图中小正方形的边长为1,则该几何体的体积为( )


| A. | $\frac{10}{3}$ | B. | 4 | C. | 6 | D. | 10 |
20.某几何体的三视图如图所示(单位:cm),则该几何体的表面积是( )
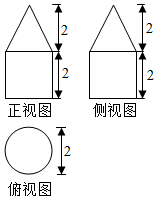

| A. | (5+$\sqrt{5}$)πcm2 | B. | (5+2$\sqrt{5}$)πcm2 | C. | (6+$\sqrt{5}$)πcm2 | D. | (6+2$\sqrt{5}$)πcm2 |
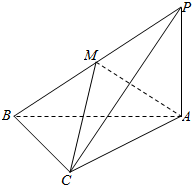 在三棱锥P-ABC中,∠PAB=∠PAC=∠ABC=90°,M是PB的中点,PA=AB=2.
在三棱锥P-ABC中,∠PAB=∠PAC=∠ABC=90°,M是PB的中点,PA=AB=2.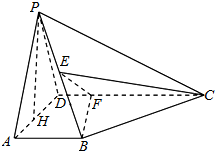 如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,E是PB的中点,F是CD上的点,PH为△PAD中AD边上的高.
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,E是PB的中点,F是CD上的点,PH为△PAD中AD边上的高.