题目内容
9.在平面直角坐标系中,圆M的方程(x-2)2+y2=1,若直线mx+y+2=0上至少存在一点P,使得以P为圆心,1为半径的圆与圆M有公共点,则m的取值范围是( )| A. | m≤0 | B. | m≤-1 | C. | m≥2 | D. | m≤-$\frac{3}{2}$ |
分析 求出圆的标准方程,根据条件确定圆心C到直线mx+y+2的距离d≤R+1=2,利用圆心到直线的距离公式进行求解即可.
解答 解:圆M的方程(x-2)2+y2=1,则圆心坐标为(2,0),半径R=1,
若直线mx+y+2=0至少存在一点,使得以该点为圆心,1为半径的圆与圆M有公共点,
则等价为圆心M到直线mx+y+2=0的距离d≤R+1=2,
即圆心到直线mx+y+2=0的距离d=$\frac{|2m+2|}{\sqrt{1+{m}^{2}}}$≤2,
解得m≤0,
故选A.
点评 本题主要考查直线和圆的位置关系的应用以及点到直线距离公式的求解,根据条件得到圆心到直线的距离关系是解决本题的关键.

练习册系列答案
相关题目
8.若a>b>0,c<d<0,则一定有( )
| A. | ac>bd | B. | ac<bd | C. | ad<bc | D. | ad>bc |
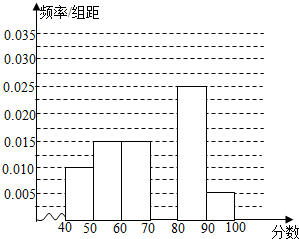 某校参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: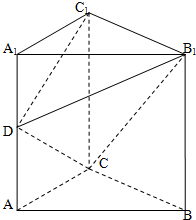 如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.
如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.