题目内容
4.已知曲线${C_1}:\left\{\begin{array}{l}x=1+cosθ\\ y=sinθ\end{array}\right.$(θ为参数),${C_2}:\left\{\begin{array}{l}x=-\frac{{\sqrt{3}}}{2}t\\ y=\frac{{2\sqrt{3}}}{3}+\frac{t}{2}\end{array}\right.$(t为参数)(1)曲线C1,C2的交点为A,B,求|AB|;
(2)以原点O为极点,x轴正半轴为极轴,建立极坐标系,过极点的直线l1与C1交于O,C两点,与直线ρsinθ=2交于点D,求$\frac{{|{OC}|}}{{|{OD}|}}$的最大值.
分析 (1)方法一:将曲线C1代入曲线C2方程,利用韦达定理及弦长公式,即可求得|AB|;
方法二:就得曲线C2的普通方程,求得交点坐标,根据三角关系,即可求得|AB|;
(2)由题意分别求得丨OC丨及丨OD丨根据二倍角公式,及三角函数的性质即可求得$\frac{{|{OC}|}}{{|{OD}|}}$的最大值.
解答 解:(1)方法一:曲线${C_1}:{(x-1)^2}+{y^2}=1$,${(-\frac{{\sqrt{3}}}{2}t-1)^2}+{(\frac{{2\sqrt{3}}}{3}+\frac{t}{2})^2}=1,{t^2}+\frac{{5\sqrt{3}}}{3}t+\frac{4}{3}=0$,
由韦达定理可知:t1+t2=-$\frac{5\sqrt{3}}{3}$,t1t2=$\frac{4}{3}$,
∴$|{AB}|=|{{t_1}-{t_2}}|=\sqrt{{{({t_1}+{t_2})}^2}-4{t_1}{t_2}}=\sqrt{3}$.
法二:C2为$y=-\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}$,过(2,0),C1过(2,0),不妨令A(2,0),
则∠OBA=90,∠OAB=30,
所以$|{AB}|=2×\frac{{\sqrt{3}}}{2}=\sqrt{3}$.
(2)C1的极坐标方程为ρ=2cosθ,令l1的极角为α,则$|{OD}|={ρ_1}=\frac{2}{sinα},|{OC}|={ρ_2}=2cosα$,
$\frac{{|{OC}|}}{{|{OD}|}}=sinαcosα=\frac{1}{2}sin2α≤\frac{1}{2}$,
∴当$α=\frac{π}{4}$时取最大值,
$\frac{{|{OC}|}}{{|{OD}|}}$的最大值$\frac{1}{2}$.
点评 本题考查直线的参数方程,考查参数方程与普通方程的转化,三角函数的性质,考查计算能力,属于中档题.

 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案| A. | (1,2) | B. | (-∞,1]∪[2,+∞) | C. | (-∞,3]∪[6,+∞) | D. | (3,6) |
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
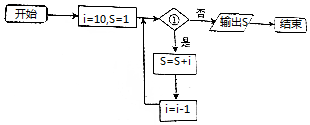
| A. | (5,6] | B. | [5,6) | C. | (6,7] | D. | [6,7) |
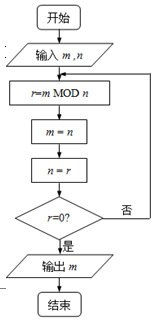 右边程序框图的算法思路源于数学名著《几何原本》中的“辗转
右边程序框图的算法思路源于数学名著《几何原本》中的“辗转