题目内容
17.求过点P(8,-2)且与直线x+y+1=0垂直的直线方程.分析 根据已知,与直线x+y+1=0垂直的直线方程的斜率k=1,从而可求出直线方程为x-y-10=0
解答 解:∵与直线x+y+1=0垂直的直线方程的斜率k=1,
∴过点P(8,-2)且与直线x+y+1=0垂直的直线方程:y+2=x-8,整理,得x-y-10=0.
点评 本题考查直线方程的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
7.若存在过点(1,0)的直线与曲线y=x3和y=ax2+$\frac{15}{4}$x-9都相切,则a的值为( )
| A. | -1或-$\frac{25}{64}$ | B. | -$\frac{23}{38}$ | C. | -2 | D. | -3或-$\frac{3}{2}$ |
6.设点A在-150°角的终边上,|$\overrightarrow{OA}$|=2$\sqrt{2}$(O是坐标原点),则向量$\overrightarrow{OA}$的坐标为( )
| A. | ($\sqrt{6}$,$\sqrt{2}$) | B. | ($\sqrt{2}$,$\sqrt{6}$) | C. | (-$\sqrt{2}$,-$\sqrt{6}$) | D. | (-$\sqrt{6}$,-$\sqrt{2}$) |
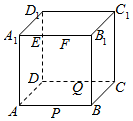 如图,正方体ABCD-A1B1C1D1的棱长为4,动点E,F在棱A1B1上,动点P,Q分别在棱AB,CD上,若EF=2,现有以下五种说法:
如图,正方体ABCD-A1B1C1D1的棱长为4,动点E,F在棱A1B1上,动点P,Q分别在棱AB,CD上,若EF=2,现有以下五种说法: