题目内容
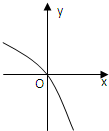已知函数f（x）的定义域为R，f′（x）为f（x）的导函数，函数y=f′（x）的图象如图所示，且f（-2）=1，f（3）=1，则不等式f（x）＞1的解集为考点：函数的单调性与导数的关系
专题：导数的综合应用
分析：根据函数的单调性和导数之间的关系，即可解不等式．
解答：
解：由导数图象可知当x≥0时，f′（x）＜0，此时函数单调递减，
当x＜0时，f′（x）＞0，此时函数单调递增，
∵f（-2）=1，f（3）=1，
∴当-2＜x＜3时，f（x）＞1，
即不等式f（x）＞1的解集为（-2，3），
故答案为：（-2，3）
当x＜0时，f′（x）＞0，此时函数单调递增，
∵f（-2）=1，f（3）=1，
∴当-2＜x＜3时，f（x）＞1，
即不等式f（x）＞1的解集为（-2，3），
故答案为：（-2，3）
点评：本题主要考查函数的单调性和导数的之间的关系，根据导数符号判断函数的单调性是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
把正整数按一定的规则排成了如图所示的三角形数表．
已知F1、F2为双曲线
如图，在一个半径为3，圆心角为已知函数f(x)=
，若关于x的方程f（x）=k有两个不同的根，则实数k的取值范围是（ ）
|
| A、（-∞，1） |
| B、（-∞，2） |
| C、（1，2） |
| D、[1，2） |