题目内容
已知函数f(x)=
,若关于x的方程f(x)=k有两个不同的根,则实数k的取值范围是( )
|
| A、(-∞,1) |
| B、(-∞,2) |
| C、(1,2) |
| D、[1,2) |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:原问题等价于于函数f(x)与函数y=k的图象有两个不同的交点,在同一个坐标系中作出两个函数的图象可得答案.
解答:
解:关于x的方程f(x)=k有两个不同的实根,
等价于函数f(x)与函数y=k的图象有两个不同的交点,
作出函数的图象如下:

由图可知实数k的取值范围是(1,2)
故选:C.
等价于函数f(x)与函数y=k的图象有两个不同的交点,
作出函数的图象如下:

由图可知实数k的取值范围是(1,2)
故选:C.
点评:本题考查根的存在性和个数的判断,数形结合是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=f(x)是定义在R上的可导函数,则下列说法不正确的是( )
| A、若函数在x=x0时取得极值,则f′(x0)=0 |
| B、若f′(x0)=0,则函数在x=x0处取得极值 |
| C、若在定义域内恒有f′(x0)=0,则y=f(x)是常数函数 |
| D、函数f(x)在x=x0处的导数是一个常数 |
不等式
≥0的解为( )
| x+2 |
| x-3 |
| A、-2≤x≤3 |
| B、x≥3或x≤-2 |
| C、-2≤x<3 |
| D、x>3或x≤-2 |
i是虚数单位,若z=
,则|z|等于( )
| 1 |
| i-1 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
圆C:(x-1)2+(y+2)2=5的圆心坐标和半径分别为( )
| A、(1,2),5 | ||
| B、(1,-2),5 | ||
C、(1,-2),
| ||
D、(-1,2),
|
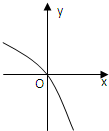 已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x)>1的解集为
已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x)>1的解集为