题目内容
已知数列{an}通项为an=ncos（
）（n∈N*），则a1+a2+a3+…+a2014= ．
| nπ |
| 2 |
考点：数列的求和
专题：点列、递归数列与数学归纳法
分析：求出an取值的规律性，得到a4k+1+a4k+2+a4k+3+a4k+4=2即可得到结论．
解答：
解：∵an=ncos（
）（n∈N*），
∴当n=4k，an=4kcos2π=4k，
当n=4k+1，an=（4k+1）cos（2π+
）=（4k+1）cos
=0，
当n=4k+2，an=（4k+2cos（2π+π）=-（4k+2），
当n=4k+3，an=（4k+3）cos（2π+
）=0，
则a4k+1+a4k+2+a4k+3+a4k+4=-（4k+2）+4k+4=2，
即a1+a2+a3+…+a2014=503（a1+a2+a3+a4）+a2013+a2014=2×503+2013cos
+2014os
=1006-2014=-1008，
故答案为：-1008
| nπ |
| 2 |
∴当n=4k，an=4kcos2π=4k，
当n=4k+1，an=（4k+1）cos（2π+
| π |
| 2 |
| π |
| 2 |
当n=4k+2，an=（4k+2cos（2π+π）=-（4k+2），
当n=4k+3，an=（4k+3）cos（2π+
| 3π |
| 2 |
则a4k+1+a4k+2+a4k+3+a4k+4=-（4k+2）+4k+4=2，
即a1+a2+a3+…+a2014=503（a1+a2+a3+a4）+a2013+a2014=2×503+2013cos
| 2013π |
| 2 |
| 2014π |
| 2 |
故答案为：-1008
点评：本题主要考查数列和的计算，根据条件利用分组求和法是解决本题的关键．
练习册系列答案
相关题目
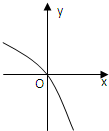已知函数f（x）的定义域为R，f′（x）为f（x）的导函数，函数y=f′（x）的图象如图所示，且f（-2）=1，f（3）=1，则不等式f（x）＞1的解集为