题目内容
已知函数f(x)=
,若方程f(x)-kx=0至少有一个实根,则实数k的取值范围 .
|
考点:根的存在性及根的个数判断,分段函数的应用
专题:函数的性质及应用
分析:画出函数f(x)的图象,将问题转化为求两个函数的交点问题,列出方程组求出k即可.
解答:
解:令f(x)-kx=0,得:f(x)=kx,令y=kx,
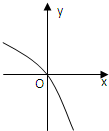
函数f(x),y=kx的图象如图示:
 ,
,
显然当y=kx与f(x)相切时有一个交点,
∴
,解得:
,
∴k≥e,
故答案为:[e,+∞).
函数f(x),y=kx的图象如图示:
 ,
,显然当y=kx与f(x)相切时有一个交点,
∴
|
|
∴k≥e,
故答案为:[e,+∞).
点评:本题考察了函数的根的存在性以及分段函数的应用,渗透了数形结合思想,是一道基础题.

练习册系列答案
相关题目
不等式
≥0的解为( )
| x+2 |
| x-3 |
| A、-2≤x≤3 |
| B、x≥3或x≤-2 |
| C、-2≤x<3 |
| D、x>3或x≤-2 |
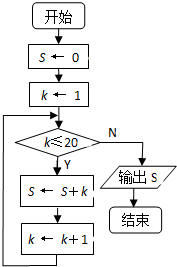
 已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x)>1的解集为
已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x)>1的解集为