题目内容
当0<x<
时,函数f(x)=
+
的最小值是 .
| π |
| 2 |
| 1 |
| sin2x |
| 16 |
| cos2x |
考点:基本不等式
专题:不等式的解法及应用
分析:由0<x<
,可得0<sin2x<1,0<cos2x<1.令sin2x=a,cos2x=b.函数f(x)=
+
?g(a,b)=
+
,a+b=1,且0<a,b<1.再利用
“乘1法”和基本不等式的性质即可得出.
| π |
| 2 |
| 1 |
| sin2x |
| 16 |
| cos2x |
| 1 |
| a |
| 16 |
| b |
“乘1法”和基本不等式的性质即可得出.
解答:
解:∵0<x<
,∴0<sin2x<1,0<cos2x<1.
令sin2x=a,cos2x=b.
则函数f(x)=
+
等价为:g(a,b)=
+
,a+b=1,且0<a,b<1.
∴g(a,b)=(a+b)(
+
)=17+
+
≥17+2
=25.当且仅当b=4a=
时取等号.
即函数f(x)=
+
的最小值是25.
故答案为:25.
| π |
| 2 |
令sin2x=a,cos2x=b.
则函数f(x)=
| 1 |
| sin2x |
| 16 |
| cos2x |
| 1 |
| a |
| 16 |
| b |
∴g(a,b)=(a+b)(
| 1 |
| a |
| 16 |
| b |
| b |
| a |
| 16a |
| b |
|
| 4 |
| 5 |
即函数f(x)=
| 1 |
| sin2x |
| 16 |
| cos2x |
故答案为:25.
点评:本题考查了问题的等价转化方法、“乘1法”和基本不等式的性质,考查了推理能力和计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=f(x)是定义在R上的可导函数,则下列说法不正确的是( )
| A、若函数在x=x0时取得极值,则f′(x0)=0 |
| B、若f′(x0)=0,则函数在x=x0处取得极值 |
| C、若在定义域内恒有f′(x0)=0,则y=f(x)是常数函数 |
| D、函数f(x)在x=x0处的导数是一个常数 |

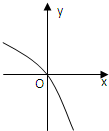 已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x)>1的解集为
已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x)>1的解集为