题目内容
2.已知$\frac{sinα-2cosα}{sinα+2cosα}$=3,计算:(1)$\frac{sinα+2cosα}{5cosα-sinα}$;
(2)(sinα+cosα)2.
分析 由已知及同角三角函数基本关系式可得:tanα=-4,利用同角三角函数基本关系式化简代入即可得解;
解答 (本题满分为12分)
解:由已知可得:sinα-2cosα=3sinα+6cosα,
可得:2sinα=-8cosα,解得:tanα=-4.
$(1)\frac{sinα+2cosα}{5cosα-sinα}=\frac{tanα+2}{5-tanα}=\frac{-4+2}{5+4}=-\frac{2}{9}$.$(2){({sinα+cosα})^2}=\frac{{{{sin}^2}α+{{cos}^2}α+2sinαcosα}}{{{{sin}^2}α+{{cos}^2}α}}=\frac{{{{tan}^2}α+1+2tanα}}{{{{tan}^2}+1}}=\frac{16+1-8}{16+1}=\frac{9}{17}$.
点评 本题主要考查了同角三角函数基本关系式的应用,考查了计算能力和转化思想,属于基本知识的考查.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
12.平面α∩β=l,直线m?α,直线n?β,则m,n的位置关系是( )
| A. | 异面 | B. | 平行 | C. | 相交 | D. | 无法确定 |
10.已知中心在原点的椭圆C以抛物线y2=4x的焦点F为右焦点,且它们的公共点P到点F的距离为$\frac{5}{3}$,则椭圆C的标准方程为( )
| A. | $\frac{{x}^{2}}{4}$+y2=1 | B. | $\frac{{y}^{2}}{4}$+x2=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 |
7.若偶函数f(x)在[0,2]上单调递减,则( )
| A. | f(-1)>f $({{{log}_{0.5}}\frac{1}{4}})$>f(lg0.5) | B. | f(lg0.5)>f(-1)>f $({{{log}_{0.5}}\frac{1}{4}})$ | ||
| C. | f $({{{log}_{0.5}}\frac{1}{4}})$>f(-1)>f(lg0.5) | D. | f(lg0.5)>f $({{{log}_{0.5}}\frac{1}{4}})$>f(-1) |
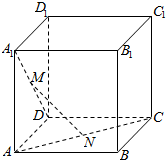 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点. 在正方体ABCD-A1B1C1D1中,P、Q、R分别在棱AB、BB1、CC1上,且PD、QR相交于点O.求证:O、B、C三点共线.
在正方体ABCD-A1B1C1D1中,P、Q、R分别在棱AB、BB1、CC1上,且PD、QR相交于点O.求证:O、B、C三点共线.