题目内容
5.已知函数$f(x)=\frac{lnx}{x+a}({a∈R})$.(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直,求a的值;
(2)讨论方程f(x)=1的实根的情况.
分析 (1)求出函数的导数,根据f′(1)=1,求出a的值即可;(2)得到a=lnx-x,通过讨论a的范围结合函数的单调性判断方程根的情况.
解答 解:(1)由题意得:f′(x)=$\frac{\frac{x+a}{x}-lnx}{{(x+a)}^{2}}$,
故f′(1)=$\frac{1+a}{{(1+a)}^{2}}$=$\frac{1}{1+a}$,
由曲线y=f(x)在点(1,f(1))处的曲线与直线x+y+1=0垂直,得:f′(1)=1,
故$\frac{1}{1+a}$=1,解得:a=0;
(2)方程f(x)=1即$\frac{lnx}{x+a}$=1,a=lnx-x,(x≠-a),
当x=-a时,得:a=ln(-a)-(-a),解得:a=-1,
a=-1时,解得:x=1,当x≠-a,即x≠1,故a=-1时,方程无实数根,
令g(x)=lnx-x,(x>0),则g′(x)=$\frac{1-x}{x}$,(x>0),
故x∈(0,1)时,g(x)是递增函数,x∈(1,+∞)时,g(x)是递减函数,
故g(x)≤g(1))=-1,
a<-1时,由ea∈(0,1),得:g(ea)=lnea-ea=a-ea<a,
又e-a∈(1,+∞),令h(x)=ex-2x,则h′(x)=ex-2,
在区间(1,+∞)上h′(x)>0,h(x)递增,
故h(x)>h(1)>0,即ex>2x,故e-a>-2a,
故g(e-a)=-a-e-a<-a-(-2a)=a,
故a<-1时,方程有2个实数根,
当a≥-1时,方程无实数根.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.

练习册系列答案
相关题目
20.全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下:
(1)根据所给统计表和频率分布直方图中的信息求出n,m的值,并完成頻率分布直方图:
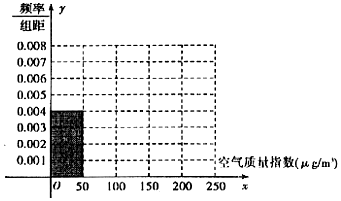
(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
| 空气质量指数(μg/m3) | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |

(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
17.若存在t∈R与正数m,使F(t-m)=F(t+m)成立,则称“函数F(x)在x=t处存在距离为2m的对称点”,设f(x)=$\frac{{x}^{2}+λ}{x}$(x>0),若对于任意t∈($\sqrt{2}$,$\sqrt{6}$),总存在正数m,使得“函数f(x)在x=t处存在距离为2m的对称点”,则实数λ的取值范围是( )
| A. | (0,2] | B. | (1,2] | C. | [1,2] | D. | [1,4] |
13.若实数x,y满足$\left\{\begin{array}{l}{x-y+1>0}\\{2x-y<0}\end{array}\right.$,则点P(x,y)不可能落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 的值是( )
的值是( ) B.
B. C.
C. D.
D.