题目内容
5.已知函数f(x)=$\frac{9}{8cos2x+16}$-sin2x,则当f(x)取最小值时cos2x的值为$-\frac{1}{2}$.分析 利用二倍角公式化简函数的表达式,利用基本不等式求解表达式的最值即可.
解答 解:函数f(x)=$\frac{9}{8cos2x+16}$-sin2x=$\frac{\frac{9}{8}}{cos2x+2}$+$\frac{cos2x+2}{2}$-$\frac{3}{2}$,∵cos2x+2>0,
∴f(x)≥2$\sqrt{\frac{\frac{9}{8}}{cos2x+2}•\frac{cos2x+2}{2}}$$-\frac{3}{2}$=2×$\frac{3}{4}-\frac{3}{2}$=0,
当且仅当$\frac{\frac{9}{8}}{cos2x+2}$=$\frac{cos2x+2}{2}$,即cos2x=-$\frac{1}{2}$时等号成立.
故答案为:-$\frac{1}{2}$.
点评 本题考查基本不等式在最值中的应用,考查计算能力.

练习册系列答案
相关题目
10.下列点在曲线x2+y2-3xy+2=0上的是( )
| A. | $(0,\sqrt{2})$ | B. | $(\sqrt{2},0)$ | C. | $(-\sqrt{2},\sqrt{2})$ | D. | $(\sqrt{2},\sqrt{2})$ |
15.已知x,y为正实数,且x+y+$\frac{1}{x}$+$\frac{1}{y}$=5,则x+y的最大值是( )
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
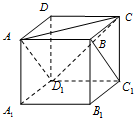 在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动,则下列四个命题:
在正方体ABCD-A1B1C1D1中(如图),已知点P在直线BC1上运动,则下列四个命题: