题目内容
1．在各项均为正数的等比数列{an}中，a2，a4+2．a5成等差数列，a1=2，Sn是数列{an}的前n项的和，则S10-S4=（ ）| A． | 1008 | B． | 2016 | C． | 2032 | D． | 4032 |
分析 利用等差数列的性质及等比数列的通项公式求出公比，由此利用等比数列前n项和公式能求出结果．
解答 解：∵在各项均为正数的等比数列{an}中，a2，a4+2．a5成等差数列，a1=2，
∴2（2q3+2）=2q+2q4，
∴2（q3+1）=q（q3+1），
由q＞0，解得q=2，
∴S10-S4=$\frac{2（1-{2}^{10}）}{1-2}$-$\frac{2（1-{2}^{4}）}{1-2}$=2016．
故选：B．
点评 本题考查等比数列前n项和，是基础题，解题时要认真审题，注意等差数列和等比数列的通项公式的合理运用．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
16．函数f（x）=x|x|是（ ）
| A． | 偶函数且增函数 | B． | 偶函数且减函数 | C． | 奇函数且增函数 | D． | 奇函数且减函数 |
6．设抛物线y=ax2+bx+c（a＞0）与x轴有两个交点A，B，顶点为C，设△=b2-4ac，∠ACB=θ，则cosθ=（ ）
| A． | $\frac{△-4}{△+4}$ | B． | $\frac{\sqrt{△}-2}{\sqrt{△}+2}$ | C． | $\frac{△+4}{△-4}$ | D． | $\frac{\sqrt{△}+2}{\sqrt{△}-2}$ |
10．在正方体ABCD-A1B1C1D1中，E、F分别为AB、C1D1的中点，则A1B1与平面A1EF夹角的正弦值为（ ）
| A． | $\frac{\sqrt{6}}{2}$ | B． | $\frac{\sqrt{6}}{3}$ | C． | $\frac{\sqrt{6}}{4}$ | D． | $\sqrt{2}$ |
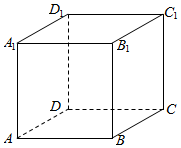如图所示，在棱长为1的正方体ABCD-A1B1C1D1中．