已知点A(4.0).抛物线C:y2=2px的焦点为F.点P在C上.△PFA为正三角形.则p=$\frac{8}{5}$．题目和参考答案——青夏教育精英家教网—

题目内容

1．已知点A（4，0），抛物线C：y²=2px（0＜p＜4）的焦点为F，点P在C上，△PFA为正三角形，则p=$\frac{8}{5}$．

分析根据抛物线的焦点，结合等边三角形的性质，运用中点坐标公式，求出P的坐标，代入抛物线的方程，解方程可得p的值．

解答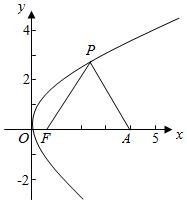解：抛物线C：y²=2px（0＜p＜4）的焦点为F（$\frac{p}{2}$，0），
可得|AF|=4-$\frac{p}{2}$，
由△PFA为等边三角形，可得P（$\frac{1}{2}$（4+$\frac{p}{2}$），$\frac{\sqrt{3}}{2}$（4+$\frac{p}{2}$）），
代入抛物线的方程，可得$\frac{3}{4}$（4+$\frac{p}{2}$）²=2p•$\frac{1}{2}$（4+$\frac{p}{2}$），
化为5p²+112p-192=0，
解得p=$\frac{8}{5}$或-24（舍去），
故答案为：$\frac{8}{5}$．

点评本题考查了抛物线的方程的应用，等边三角形的性质，考查运算能力，比较基础．

练习册系列答案

12．已知数列{a_n}的前n项和为S_n，S_n=2a_n-1，数列{b_n}为等差数列，且 b₁=a₁，b₆=a₅
（1）求数列{a_n}与{b_n}的通项公式；
（2）若C_n=a_nb_n，求数列{c_n}的前n项和T_n．

9．已知函数f（x）=2x²+bx+c，不等式f（x）＜0的解集是（0，5），若对于任意x∈[2，4]，不等式f（x）+t≤2恒成立，则t的取值范围为（-∞，10]．

16．设a、b是两条不同的直线，α、β是两个不同的平面，则下面四个命题中不正确的是（　　）

	A．	若a⊥b，a⊥α，b?α，则b∥α		B．	若a⊥b，a⊥α，b⊥β，则α⊥β
	C．	若a∥α，α⊥β，则α⊥β		D．	若a⊥β，α⊥β，则a∥α

6．某单位有8名员工，其中有5人曾经参加过技能培训，另外3人没有参加过任何培训，现要从8名员工中任选3人参加一种新的技能培训．
（Ⅰ）求恰好选到1名曾经参加过技能培训的员工的概率；
（Ⅱ）这次培训结束后，仍然没有参加过任何培训的员工数ξ是一个随机变量，求ξ的分布列和数学期望Eξ．

13．已知函数f（x）=|x²-2ax+b|（x∈R），给出下列命题：
①若a²-b≤0，则f（x）在区间[a，+∞）上是增函数；
②?a∈R，使f（x）为偶函数；
③若f（0）=f（2），则f（x）的图象关于x=1对称；
④若a²-b-2＞0，则函数h（x）=f（x）-2有2个零点．
其中正确命题的序号为①②．