题目内容
| a |
| x2 |
| 3 |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：平面向量数量积的运算
专题：函数的性质及应用,导数的综合应用,平面向量及应用
分析：运用向量的数量积的坐标表示和函数的导数，求出单调区间和最小值，再由向量的夹角公式和夹角的范围，计算即可得到．
解答：
解：由
=（
，x），
=（x，x-3），x≥-4，
则
•
=
+x2-3x，
可令y=
+x2-3x，y′=x2+2x-3，
当-4≤x＜-3和x＞1时，y′＞0，函数y递增；
当-3＜x＜1时，y′＜0，函数y递减．
由f（-4）=-
+16+12＞0，f（1）=
+1-3＜0，
则x=1时，
•
取最小值．
即有
=（
，1），
=（1，-2），
cos＜
，
＞=
=
=-
，
由0≤＜
，
＞≤π，
则＜
，
＞=
．
故选：C．
| a |
| x2 |
| 3 |
| b |
则
| a |
| b |
| x3 |
| 3 |
可令y=
| x3 |
| 3 |
当-4≤x＜-3和x＞1时，y′＞0，函数y递增；
当-3＜x＜1时，y′＜0，函数y递减．
由f（-4）=-
| 64 |
| 3 |
| 1 |
| 3 |
则x=1时，
| a |
| b |
即有
| a |
| 1 |
| 3 |
| b |
cos＜
| a |
| b |
| ||||
|
|
| ||||||
|
| ||
| 2 |
由0≤＜
| a |
| b |
则＜
| a |
| b |
| 3π |
| 4 |
故选：C．
点评：本题考查向量的数量积的坐标表示和夹角公式，主要考查导数的运用：求单调性和极值、最值，属于中档题．
练习册系列答案
相关题目
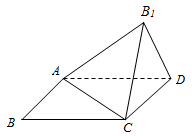已知四边形ABCD是矩形，BC=kAB（k∈R），将△ABC沿着对角线AC翻折，得到△AB1C，设顶点B1在平面ABCD上的投影为O．