题目内容
对于c>0,当非零实数a、b满足a2-2ab+2b2=c且使|a+b|最大时,
-
+
的最小值为 .
| 3 |
| a |
| 4 |
| b |
| 5 |
| c |
考点:二维形式的柯西不等式
专题:计算题,不等式的解法及应用
分析:首先把:a2-2ab+2b2=c,转化为c=(a-b)2+b2,再由柯西不等式得到|a+b|2,分别用b表示a,c,在代入到
-
+
得到关于b的函数,求出最小值即可.
| 3 |
| a |
| 4 |
| b |
| 5 |
| c |
解答:
解:∵a2-2ab+2b2=c,
∴c=(a-b)2+b2,
由柯西不等式得,[(a-b)2+b2](1+4)≥|a+b|2
故当|a+b|最大时,有a-b=
∴a=
b,c=
b2
∴
-
+
=
-
=4(
-
)2+
当b=4时,取得最小值为
.
故答案为:
.
∴c=(a-b)2+b2,
由柯西不等式得,[(a-b)2+b2](1+4)≥|a+b|2
故当|a+b|最大时,有a-b=
| b |
| 2 |
∴a=
| 3 |
| 2 |
| 5 |
| 4 |
∴
| 3 |
| a |
| 4 |
| b |
| 5 |
| c |
| 4 |
| b2 |
| 2 |
| b |
| 1 |
| b |
| 1 |
| 4 |
| 1 |
| 4 |
当b=4时,取得最小值为
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查了柯西不等式,以及二次函数的最值问题,属于难题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知向量
=(4,0),B是圆C:(x-
)2+(y-
)2=1上的一个动点,则两向量
与
所成角的最大值为( )
| OA |
| 2 |
| 2 |
| OA |
| OB |
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合M={y|y=|cos2x-sin2x|,x∈R},N={x|y=ln(1-x2)},则M∩N=( )
| A、{x|-1≤x≤1} |
| B、{x|-1≤x≤0} |
| C、{x|0<x≤1} |
| D、{x|0≤x<1} |
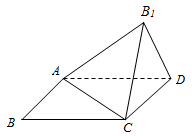 已知四边形ABCD是矩形,BC=kAB(k∈R),将△ABC沿着对角线AC翻折,得到△AB1C,设顶点B1在平面ABCD上的投影为O.
已知四边形ABCD是矩形,BC=kAB(k∈R),将△ABC沿着对角线AC翻折,得到△AB1C,设顶点B1在平面ABCD上的投影为O. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.