题目内容
已知函数f(x)=g(x)•e-x在x=
处有极值,则函数y=g(x)的图象可能是( )
| π |
| 6 |
A、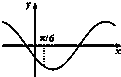 |
B、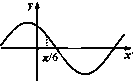 |
C、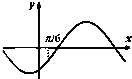 |
D、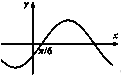 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:函数的性质及应用,导数的综合应用
分析:先对f(x)求导,再利用极值的性质,得到f′(
)=0,即g′(
)=g(
),由导数的几何意义得在x=
处的导数值即切线的斜率,等于
的函数值,再对选项一一加以判断,即可得到A正确,B,C,D均错.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
解答:
解:函数f(x)=g(x)•e-x在的导数f′(x)=g′(x)•e-x+g(x)•e-x•(-1)
=e-x•(g′(-x)-g(x)),
由于函数f(x)=g(x)•e-x在x=
处有极值,
则f′(
)=0,即有g′(
)-g(
)=0,即g′(
)=g(
),
由导数的几何意义得在x=
处的导数值即切线的斜率,等于
的函数值,
对于A.在x=
处的切线的斜率为负值,函数值也为负,故A正确;
对于B.在x=
处的切线的斜率为负值,函数值为正,故B错;
对于C.在x=
处的切线的斜率为正值,函数值为负,故C错;
对于D.在x=
处的切线的斜率为正值,函数值为0,故D错.
故选A.
=e-x•(g′(-x)-g(x)),
由于函数f(x)=g(x)•e-x在x=
| π |
| 6 |
则f′(
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
由导数的几何意义得在x=
| π |
| 6 |
| π |
| 6 |
对于A.在x=
| π |
| 6 |
对于B.在x=
| π |
| 6 |
对于C.在x=
| π |
| 6 |
对于D.在x=
| π |
| 6 |
故选A.
点评:本题考查导数的几何意义:曲线在某点处的切线的斜率,考查极值的概念及运用,考查判断能力和观察能力,属于中档题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
已知椭圆的两焦点F1,F2在x轴上,|F1F2|=4
,P为椭圆上一点,且|PF1|=
,|PF2|=
,则此椭圆的标准方程为( )
| 2 |
| 7 |
| 2 |
| 5 |
| 2 |
A、
| ||
B、x2+
| ||
C、
| ||
D、x2+
|
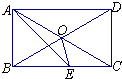 如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则以下结论:①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,⑤∠AEO=30°其中正确的有( )
如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则以下结论:①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,⑤∠AEO=30°其中正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
已知直线l:2x+3y+1=0被圆C:x2+y2=1所截得的弦长为d,则下列直线中被圆C截得的弦长同样为d的直线是( )
| A、2x+4y-1=0 |
| B、2x+3y-1=0 |
| C、4x+3y-1=0 |
| D、3x+2y=0 |
集合A={a2,a+1,-1},B={2a-1,|a-2|,3a2-4},A∩B={-1},则a的值是( )
| A、±1 | B、0,或±1 |
| C、0,1 | D、0,-1 |