题目内容

17．以下四个命题中，其中真命题的个数为（　　）
①在回归分析中，可用相关指数R2的值判断模型的拟合效果，R2越大，模拟的拟合效果越好；
②两个随机变量的线性相关性越强，相关系数越接近于1；
③若数据x1，x2，x3…，xn的方差为1，则3x1，3x2，3x3…，3xn的方差为3；
④对分类变量x与y的随机变量的观测值k2来说，k越小，判断“x与y有关系”的把握程度越大．
A．1B．2C．3D．4

分析 （1）根据相关指数R2的值的性质进行判断，
（2）根据线性相关性与r的关系进行判断，
（3）根据方差关系进行判断，
（4）根据分类变量x与y的随机变量k2的观察值的关系进行判断．

解答 解：（1）用相关指数R2的值判断模型的拟合效果，R2越大，模型的拟合效果越好，故（1）正确；
（2）若两个随机变量的线性相关性越强，则相关系数r的绝对值越接近于1，故（2）错误；
（3）若统计数据x1，x2，x3，…，xn的方差为1，则3x1，3x2，3x3…，3xn的方差为9，故（3）错误；
（4）对分类变量x与y的随机变量k2的观察值k2来说，k越小，判断“x与y有关系”的把握程度越大．错误；
故选：A．

点评 本题主要考查命题的真假判断，涉及概率统计中随机变量的关系及随机变量的相关性研究回归直线方程的概念，考查了推理能力，属于基础题．

练习册系列答案
相关题目
7．下列几种推理过程是演绎推理的是（　　）
A．5和ln3可以比较大小
B．由平面三角形的性质，推测空间四面体的性质
C．东升高中高二年级有15个班，1班有51人，2班有53人，3班有52人，由此推测各班都超过50人
D．预测股票走势图
8．运行如图所示的程序框图，则输出的a、b、c满足（　　）
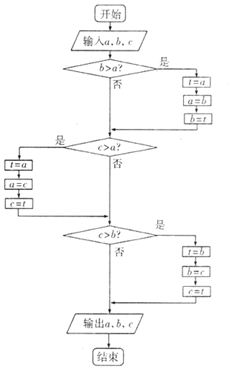
A．c≤b≤aB．a≤b≤cC．a≤c≤bD．b≤c≤a
5．设直线l：3x+4y+4=0，圆C：（x-2）2+y2=r2（r＞0），若圆C上存在两点P，Q，直线l上存在一点M，使得∠PMQ=90°，则r的取值范围是$[\sqrt{2}，+∞）$．
12．若实数x，y满足约束条件$\left\{\begin{array}{l}2x-y-2≤0\\ 2x+y-4≥0\\ y≤2\end{array}\right.$则$\frac{y}{x}$的取值范围是  （　　）
A．$[{\frac{2}{3}，2}]$B．$[{\frac{1}{2}，\frac{3}{2}}]$C．$[{\frac{3}{2}，2}]$D．[1，2]
2．如图所示，图中粗线画出的是某几何体的三视图，该几何体的体积是（　　）
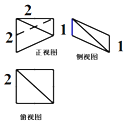
A．$\frac{2}{3}$B．$\frac{4}{3}$C．$\frac{8}{3}$D．4
9．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率是$\frac{1}{2}$，过点$P（0，\frac{{\sqrt{3}}}{2}）$的动直线l与椭圆相交于A，B两点，当直线l平行与x轴时，直线l被椭圆截得的线段长为$2\sqrt{3}$．（F1，F2分别为左，右焦点）
（1）求椭圆的标准方程；
（2）过F2的直线l′交椭圆于不同的两点M，N，则△F1MN内切圆的面积是否存在最大值？若存在，求出这个最大值及此时的直线l′方程；若不存在，请说明理由．
6．已知$\overrightarrow a=（{\sqrt{3}sinx，cosx+sinx}），\overrightarrow b=（{2cosx，sinx-cosx}），f（x）=\overrightarrow a•\overrightarrow b$．
（1）求函数f（x）的单调区间；
（2）当$x∈[{\frac{5π}{24}，\frac{5π}{12}}]$时，对任意的t∈R，不等式mt2+mt+3≥f（x）恒成立，求实数m的取值范围．
7．2017年某市开展了“寻找身边的好老师”活动，市六中积极行动，认真落实，通过微信关注评选“身边的好老师”，并对选出的班主任工作年限不同的五位“好老师”的班主任的工作年限和被关注数量进行了统计，得到如下数据：
班主任工作年限x（单位：年）4681012
被关注数量y（单位：百人）1020406050
（1）若”好老师”的被关注数量y与其班主任的工作年限x满足线性回归方程，试求回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，并就此分析：“好老师”的班主任工作年限为15年时被关注的数量；
（2）若用$\frac{y_i}{x_i}$（i=1，2，3，4，5）表示统计数据时被关注数量的“即时均值”（四舍五入到整数），从“即时均值”中任选2组，求这2组数据之和小于8的概率．（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网