题目内容
5.设直线l:3x+4y+4=0,圆C:(x-2)2+y2=r2(r>0),若圆C上存在两点P,Q,直线l上存在一点M,使得∠PMQ=90°,则r的取值范围是$[\sqrt{2},+∞)$.分析 由切线的对称性和圆的知识将问题转化为MC⊥l时,使得过M作圆的两条切线,切线夹角大于等于900即可.
解答 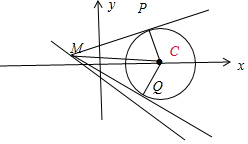 解:圆C:(x-2)2+y2=r2,圆心为:(2,0),半径为r,
解:圆C:(x-2)2+y2=r2,圆心为:(2,0),半径为r,
∵在圆C上存在两点P,Q,在直线l上存在一点M,使得∠PMQ=90°,
∴在直线l上存在一点M,使得过M作圆的两条切线,切线夹角大于等于90,
∴只需MC⊥l时,使得过M作圆的两条切线,切线夹角大于等于900即可
∵C到直线l:3x+4y+4=0的距离2,则r$≥2×sin4{5}^{0}=\sqrt{2}$.
个答案为:[$\sqrt{2}$,+∞).
点评 本题考查直线和圆的位置关系,转化思想是解决问题的关键,属中档题

练习册系列答案
相关题目
16.如图是某产品加工为成品的流程图,从图中可以看出,若是一件废品,则必须至少经过的工序数目为( )


| A. | 6道 | B. | 5道 | C. | 4道 | D. | 3道 |
20.执行如图的程序框图,若输入的n为6,则输出的p为( )
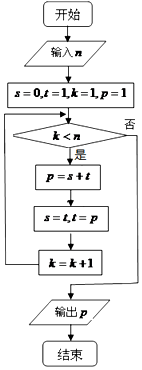

| A. | 8 | B. | 13 | C. | 29 | D. | 35 |
14.如果某四棱锥的三视图如图所示,那么该四棱锥的四个侧面中是直角三角形的有( )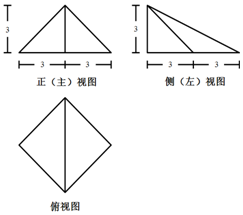

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |