题目内容
ABCD-A1B1C1D1是正方体，点O为正方体对角线的交点，过点O的任一平面α，正方体的八个顶点到平面α的距离作为集合A的元素，则集合A中的元素个数最多为
- A.3个
- B.4个
- C.5个
- D.6个
B
分析：根据题意，由正方体的结构特点，可得O是线段A1C的中点，过点O作任一平面α，设A1C与α所成的角为θ，分析可得点A1与C到平面α的距离相等，同理可得B与D1，A与C1，D与B1到平面α的距离相等，则可得集合A中的元素个数最多为4个，即可得答案．
解答：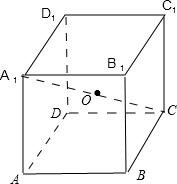
解：根据题意，如图，点O为正方体对角线的交点，则O是线段A1C的中点，
过点O作任一平面α，设A1C与α所成的角为θ，
分析可得点A1与C到平面α的距离相等，均为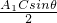
，
同理B与D1到平面α的距离相等，
A与C1到平面α的距离相等，
D与B1到平面α的距离相等，
则集合A中的元素个数最多为4个；
故选B．
点评：本题考查正方体的几何结构，注意正方体中心的性质，即体对角线的交点，从而分析得到体对角线的两个端点到平面α的距离相等．
分析：根据题意，由正方体的结构特点，可得O是线段A1C的中点，过点O作任一平面α，设A1C与α所成的角为θ，分析可得点A1与C到平面α的距离相等，同理可得B与D1，A与C1，D与B1到平面α的距离相等，则可得集合A中的元素个数最多为4个，即可得答案．
解答：
解：根据题意，如图，点O为正方体对角线的交点，则O是线段A1C的中点，过点O作任一平面α，设A1C与α所成的角为θ，
分析可得点A1与C到平面α的距离相等，均为
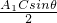，同理B与D1到平面α的距离相等，
A与C1到平面α的距离相等，
D与B1到平面α的距离相等，
则集合A中的元素个数最多为4个；
故选B．
点评：本题考查正方体的几何结构，注意正方体中心的性质，即体对角线的交点，从而分析得到体对角线的两个端点到平面α的距离相等．
练习册系列答案
相关题目
已知长方体ABCD-A1B1C1D1中，棱AB=BC=3，BB1=4，连接B1C，在CC1上有点E，使得A1C⊥平面EBD，BE交B1C于F．
在边长为a的正方体ABCD-A1B1C1D1中，E、F分别为AB与C1D1的中点．
（1）求证：四边形A1ECF是菱形；
（2）求证：EF⊥平面A1B1C；
（3）求A1B1与平面A1ECF所成角的正切值．
（1）求证：四边形A1ECF是菱形；
（2）求证：EF⊥平面A1B1C；
（3）求A1B1与平面A1ECF所成角的正切值．
如图，M，N，K分别是正方体ABCD-A1B1C1D1的棱AB，CD，C1D1的中点．
如图，已知长方体ABCD-A1B1C1D1，AB=BC=1，BB1=2，连接B1C，过B点作B1C．已知正四棱柱ABCD―A1B1C1D1中，AB=2，AA1=3.
（I）求证：A1C⊥BD；
（II）求直线A1C与侧面BB1C1C所成的角的正切值；
|