题目内容
地球北纬45°圈上有A，B两地，分别在东经120°和西经150°处，若地球半径为R，则A，B两地的球面距离为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：球面距离及相关计算
专题：计算题,空间位置关系与距离
分析：由于甲、乙两地在同一纬度圈上，计算经度差，求出甲、乙两地对应的AB弦长，以及球心角，然后求出球面距离．
解答：
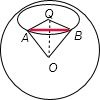解：地球表面上从甲地（北纬45°，东经120°）到乙地（北纬45°，西经150°）
甲、乙两地对应的AB的纬圆半径是
，经度差是90°，
所以AB=R
所以球心角是
，
所以甲、乙两地的球面距离是
．
故选：B．
解：地球表面上从甲地（北纬45°，东经120°）到乙地（北纬45°，西经150°）甲、乙两地对应的AB的纬圆半径是
| ||
| 2 |
所以AB=R
所以球心角是
| π |
| 3 |
所以甲、乙两地的球面距离是
| πR |
| 3 |
故选：B．
点评：本题考查球面距离及其他计算，考查空间想象能力，是基础题．
练习册系列答案
相关题目
在⊙O中，直径AB，CD互相垂直，BE切⊙O于B，且BE=BC，CE交AB于F，交⊙O于M，连结MO并延长，交⊙O于N，则下列结论中，正确的是（ ）| A、CF=FM |
| B、OF=FB |
| C、弧BM的度数为22.5° |
| D、BC∥MN |
已知c是椭圆
+
=1（a＞b＞0）的半焦距，则
的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 2b+c |
| 2a |
A、（
| ||||||
B、（
| ||||||
C、（
| ||||||
D、（
|
过抛物线y2=2px（p＞0）的焦点F的直线l与该抛物线交于A，B两点，
=3
，A，B在抛物线的准线上的射影分别为D，C．若梯形ABCD的面积为8
，则抛物线的方程为（ ）
| AF |
| FB |
| 3 |
A、y2=3
| ||
B、y2=
| ||
C、y2=
| ||
D、y2=
|
动点P（a，b）在不等式组
表示的平面区域内部及其边界上运动，则u=
的取值范围是（ ）
|
| a+b-3 |
| a-1 |
| A、（-∞，-1]∪[3，+∞） |
| B、[-1，3] |
| C、（-1，3） |
| D、（-∞，-1）∪（3，+∞） |
已知
，
，
均为单位向量，且|
+
|=1，则（
-
）•
的取值范围是（ ）
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| A、[0，1] | ||||
| B、[-1，1] | ||||
C、[-
| ||||
D、[0，
|
如图，铁路线上AB段长100千米，工厂C到铁路的距离CA为20千米．现要在AB上某一点D处，向C修一条公路，已知铁路每吨千米的运费与公路每吨千米的运费之比为3：5．为了使原料从供应站B运到工厂C的运费最少，D点应选在何处？