题目内容
16.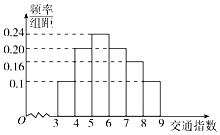 随着社会发展,襄阳市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从襄阳市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:
随着社会发展,襄阳市在一天的上下班时段也出现了堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从襄阳市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:(I)据此直方图估算交通指数的中位数和平均数;
(II)据此直方图求出早高峰一至四马路之间的3个路段至少有2个严重拥堵的概率是多少?
(III)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为35分钟,中度拥堵为45分钟,严重拥堵为60分钟,求此人用时间的数学期望.
分析 (Ⅰ)由频率分布直方图能估算交通指数的中位数和平均数.
(Ⅱ)设事件A为“1条路段严重拥堵”,则P(A)=0.1,由此能求出3条路段中至少有2条路段严重拥堵的概率.
(Ⅲ)由题意,求出所用时间X的分布列,由此能求出此人上班路上所用时间的数学期望.
解答 解:(Ⅰ)由直方图知:T∈[3,5)时,频率为0.1+0.20=0.30,
T∈[5,6)时,频率为0.24,
∴交通指数的中位数为 5+1×$\frac{0.5-0.3}{0.24}$=$\frac{35}{6}$.…(2分)
交通指数的平均数为:4.5×0.2+5.5×0.24+6.5×0.2+7.5×0.16=4.72.…(4分)
(Ⅱ)设事件A为“1条路段严重拥堵”,则P(A)=0.1,
则3条路段中至少有2条路段严重拥堵的概率为:
P=C32×($\frac{1}{10}$)2×(1-$\frac{1}{10}$)+C33×($\frac{1}{10}$)3=$\frac{7}{250}$,
所以3条路段中至少有2条路段严重拥堵的概率为$\frac{7}{250}$.…(8分)
(Ⅲ)由题意,所用时间X的分布列如下表:
| X | 30 | 35 | 45 | 60 |
| P | 0.1 | 0.44 | 0.36 | 0.1 |
所以此人上班路上所用时间的数学期望是40.6分钟.…(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,考查数据处理能力、运算求解能力,考查化归与转化思想,是中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
11.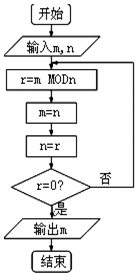 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )
 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMODn”表示m除以n的余数),若输入的m,n分别为325,125,则输出的m=( )| A. | 0 | B. | 5 | C. | 25 | D. | 45 |
1.如图1为某市2017年2月28天的日空气质量指数折线图.
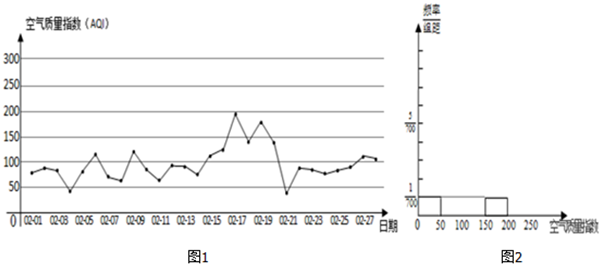
由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
(Ⅰ)请根据所给的折线图补全如图2所示的频率分布直方图(并用铅笔涂黑矩形区域),并估算该市2月份空气质量指数监测数据的平均数(保留小数点后一位);
(Ⅱ)在该月份中任取两天,求空气质量至少有一天为优或良的概率;
(Ⅲ)如果该市对环境进行治理,治理后经统计,每天的空气质量指数近似满足X~N(75,552),则治理后的空气质量指数均值大约下降了多少?

由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
(Ⅱ)在该月份中任取两天,求空气质量至少有一天为优或良的概率;
(Ⅲ)如果该市对环境进行治理,治理后经统计,每天的空气质量指数近似满足X~N(75,552),则治理后的空气质量指数均值大约下降了多少?
5.为了研究家用轿车在高速公路上的车速情况,交通部门对100名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在55名男性驾驶员中,平均车速超过100km/h的有45人,不超过100km/h的有10人;在45名女性驾驶员中,平均车速超过100km/h的有25人,不超过100km/h的有20人.
(Ⅰ)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h与性别有关;
(Ⅱ)在被调查的驾驶员中,按分层抽样的方法从平均车速不超过100km/h的人中抽取6人,再从这6人中采用简单随机抽样的方法随机抽取2人,求这2人恰好为1名男生、1名女生的概率.
参考公式与数据:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
(Ⅰ)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h与性别有关;
| 平均车速超过100km/h人数 | 平均车速不超过100km/h人数 | 合计 | |
| 男性驾驶人数 | 45 | 10 | 55 |
| 女性驾驶人数 | 25 | 20 | 45 |
| 合计 | 70 | 30 | 100 |
参考公式与数据:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| P(k2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |




 在△ABC中,角A,B,C的对边分别为a,b,c,满足$\sqrt{3}a=b(sinC+\sqrt{3}cosC)$.
在△ABC中,角A,B,C的对边分别为a,b,c,满足$\sqrt{3}a=b(sinC+\sqrt{3}cosC)$.