题目内容
写出下面数列{an}的前5项:
(1)a1=
,an=4an-1+1(n>1);
(2)a1=-
,an=1-
(n>1).
(1)a1=
| 1 |
| 2 |
(2)a1=-
| 1 |
| 4 |
| 1 |
| an-1 |
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:(1)由a1=
,an=4an-1+1(n>1),分别取n=2,3,4,5,即可得出;
(2)由a1=-
,an=1-
(n>1),分别取n=2,3,4,5,即可得出.
| 1 |
| 2 |
(2)由a1=-
| 1 |
| 4 |
| 1 |
| an-1 |
解答:
解:(1)∵a1=
,an=4an-1+1(n>1),分别取n=2,3,4,5,可得a2=4a1+1=3,a3=13,a4=40,a5=121;
(2)∵a1=-
,an=1-
(n>1),分别取n=2,3,4,5,可得a2=1-
=5,a3=
,a4=-
,a5=6.
| 1 |
| 2 |
(2)∵a1=-
| 1 |
| 4 |
| 1 |
| an-1 |
| 1 |
| a1 |
| 4 |
| 5 |
| 1 |
| 5 |
点评:本题考查了递推式的应用,考查了计算能力,属于基础题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
已知f(x)=x2+cosα,则曲线f(x)在x=
处的切线斜率为( )
| π |
| 6 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如果两个函数的图象经过平移后能够重合,那么这两个函数称为“伴侣”函数,下列函数中与g(x)=sinx+cosx能构成“伴侣”函数的是( )
A、f(x)=
| ||||||
| B、f(x)=1+sinx | ||||||
C、f(x)=sin
| ||||||
D、f(x)=2cos
|
过点P(3,1)作曲线C:x2+y2-2x=0的两条切线,切点分别为A,B,则直线AB的方程为( )
| A、2x+y-3=0 |
| B、2x-y-3=0 |
| C、4x-y-3=0 |
| D、4x+y-3=0 |
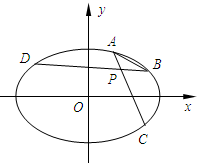 如图所示,在平面直角坐标系xOy中,设椭圆E:
如图所示,在平面直角坐标系xOy中,设椭圆E: