题目内容
5.已知α,β为锐角,且$tanα=\frac{1}{7}$,$cos({α+β})=\frac{{2\sqrt{5}}}{5}$,则cos2β=( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{{7\sqrt{2}}}{10}$ |
分析 首先由已知求出α,α+β的其它三角函数值,然后由β=α+β-α,求出β的三角函数值,再借助于倍角公式求值.
解答 解:由已知α为锐角,且$tanα=\frac{1}{7}$,得到sinα=$\frac{\sqrt{2}}{10}$,cosα=$\frac{7\sqrt{2}}{10}$,
由$cos({α+β})=\frac{{2\sqrt{5}}}{5}$,得到sin(α+β)=$\frac{\sqrt{5}}{5}$,
所以cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=$\frac{2\sqrt{5}}{5}×\frac{7\sqrt{2}}{10}+\frac{\sqrt{5}}{5}×\frac{\sqrt{2}}{10}=\frac{15\sqrt{10}}{50}=\frac{3\sqrt{10}}{10}$,
所以cos2β=2cos2β-1=$2×\frac{9}{10}-1=\frac{4}{5}$;
故选C.
点评 本题考查了三角函数式的化简求值;熟练运用两角和与差的三角函数以及角的等价变化、倍角公式是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知i为虚数单位,若z1=1+2i,z2=1-i,则复数$\frac{z_1}{z_2^2}$在复平面内对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.设集合$A=\left\{{x|{{log}_2}({{x^2}-x-4})>1}\right\}$,$B=\left\{{x|\sqrt{x-2}<2}\right\}$,则A∩B=( )
| A. | (3,6) | B. | (-∞,-2)∪(3,6) | C. | (3,4) | D. | (-∞,-2)∪(3,4) |
20.已知长方体ABCD-A1B1C1D1中,$A{A_1}=AB=\sqrt{3}$,AD=1,则异面直线B1C和C1D所成角的余弦值为( )
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}}}{6}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
17.将直角三角形ABC沿斜边上的高AD折成120°的二面角,已知直角边AB=4$\sqrt{3}$,AC=4$\sqrt{6}$,那么下面说法正确的是( )
| A. | 平面ABC⊥平面ACD | |
| B. | 四面体D-ABC的体积是$\frac{16}{3}\sqrt{6}$ | |
| C. | 二面角A-BC-D的正切值是$\frac{{\sqrt{42}}}{5}$ | |
| D. | BC与平面ACD所成角的正弦值是$\frac{{\sqrt{21}}}{14}$ |
14.已知△ABC的外接圆半径为R,角A,B,C所对的边分别为a,b,c,若asinBcosC+$\frac{3}{2}$csinC=$\frac{2}{R}$,则△ABC面积的最大值为( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{12}{5}$ |
15.已知$\frac{1}{sinφ}$+$\frac{1}{cosφ}$=2$\sqrt{2}$,若φ∈(0,$\frac{π}{2}$),则${∫}_{-1}^{tanφ}$(x2-2x)dx=( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
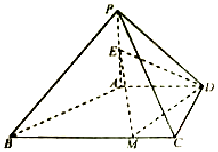 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥DC,AD=DC=PA=2,BC=4,E为PA的中点,M为棱BC上一点.