题目内容
2.已知△ABC的外接圆圆心为O,且∠A=60°,若$\overrightarrow{AO}=α\overrightarrow{AB}+β\overrightarrow{AC}(α,β∈R)$,则α+β的最大值为$\frac{2}{3}$.分析 延长AO交BC于D,设$\overrightarrow{AD}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,(m>0,n>0),由平面向量基本定理和向量共线定理可得m+n=α$\frac{|AD|}{|AO|}$+β$\frac{|AD|}{|AO|}$,由B,C,D三点共线,可得α+β=1,进而得到α+β=$\frac{1}{1+\frac{|OD|}{|OA|}}$,求出|OD|的最小值,可过O作OM⊥BC,求得|OM|即可得到所求最大值.
解答 解:延长AO交BC于D,设$\overrightarrow{AD}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,(m>0,n>0),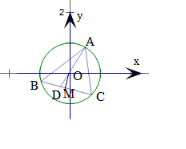
又$\overrightarrow{AO}=α\overrightarrow{AB}+β\overrightarrow{AC}(α,β∈R)$,
易得$\frac{m}{α}$=$\frac{n}{β}$=$\frac{|AD|}{|AO|}$即有m=α$\frac{|AD|}{|AO|}$,n=β$\frac{|AD|}{|AO|}$,
则m+n=α$\frac{|AD|}{|AO|}$+β$\frac{|AD|}{|AO|}$,
由B,C,D三点共线,可得m+n=1,
即有α+β=$\frac{|AO|}{|AD|}$=$\frac{|AO|}{|AO|+|OD|}$=$\frac{1}{1+\frac{|OD|}{|OA|}}$,
由于|AO|=r是定值,只需|OD|最小,
过O作OM⊥BC,垂足为M,则OD≥OM,
即有∠BOM=∠BAC,
∵∠BAC=60°,
∴cos∠BAC=$\frac{1}{2}$=$\frac{|OM|}{|OB|}$,则|OM|=$\frac{1}{2}$r.
则α+β≤$\frac{1}{1+\frac{1}{2}}$=$\frac{2}{3}$.
即有α+β的最大值为$\frac{2}{3}$.
故答案为:$\frac{2}{3}$
点评 本题考查平面向量的基本定理的运用,主要考查向量共线定理的运用和同角的基本关系式的运用,考查运算能力,属于难题.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
| A. | (3,6) | B. | (-∞,-2)∪(3,6) | C. | (3,4) | D. | (-∞,-2)∪(3,4) |
| A. | 平面ABC⊥平面ACD | |
| B. | 四面体D-ABC的体积是$\frac{16}{3}\sqrt{6}$ | |
| C. | 二面角A-BC-D的正切值是$\frac{{\sqrt{42}}}{5}$ | |
| D. | BC与平面ACD所成角的正弦值是$\frac{{\sqrt{21}}}{14}$ |
| 日销售量(枝) | 0~50 | 50~100 | 100~150 | 150~200 | 200~250 |
| 销售天数 | 3天 | 5天 | 13天 | 6天 | 3天 |
(2)若此花店在日销售量低于100枝的时候选择2天作促销活动,求这2天恰好是在日销售量低于50枝时的概率.
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{12}{5}$ |