题目内容
3.在△ABC中,角A、B、C所对的边分别为a、b、c,且$\frac{\sqrt{3}a}{cosA}$=$\frac{b}{sinB}$.(Ⅰ)求角A的值;
(Ⅱ)若B=$\frac{π}{6}$,且△ABC的面积为4$\sqrt{3}$,求BC边上的中线AM的大小.
分析 (Ⅰ)由正弦定理,同角三角函数基本关系式可求tanA,结合范围A∈(0,π),可得A的值.
(Ⅱ)由题意设AC=BC=2a,利用三角形面积公式可求a的值,在△ACM中,由余弦定理即可求得AM的值.
解答 解:(Ⅰ)由正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}$,又由已知$\frac{\sqrt{3}a}{cosA}=\frac{b}{sinB}$,
所以$\frac{\sqrt{3}a}{cosA}=\frac{a}{sinA}$,tanA=$\frac{\sqrt{3}}{3}$,
因为A∈(0,π),所以A=$\frac{π}{6}$.
(Ⅱ)由已知B=$\frac{π}{6}$,则△ABC是等腰三角形,∠C=$\frac{2π}{3}$,设AC=BC=2a,
S△ABC=$\frac{1}{2}AC•BC•sin∠ACB$=$\frac{1}{2}•(2a)^{2}sin\frac{2π}{3}$=$\sqrt{3}$a2,
由已知△ABC的面积为4$\sqrt{3}$,得a2=4,a=2,
△ACM中,由余弦定理,AM2=CA2+CM2-2CA•CM•cos$\frac{2π}{3}$
=42+22-2×2×4×(-$\frac{1}{2}$)=28,
所以AM=2$\sqrt{7}$.
点评 本题主要考查了正弦定理,同角三角函数基本关系式,三角形面积公式,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
13.设集合$A=\left\{{x|{{log}_2}({{x^2}-x-4})>1}\right\}$,$B=\left\{{x|\sqrt{x-2}<2}\right\}$,则A∩B=( )
| A. | (3,6) | B. | (-∞,-2)∪(3,6) | C. | (3,4) | D. | (-∞,-2)∪(3,4) |
14.已知△ABC的外接圆半径为R,角A,B,C所对的边分别为a,b,c,若asinBcosC+$\frac{3}{2}$csinC=$\frac{2}{R}$,则△ABC面积的最大值为( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{12}{5}$ |
18.已知函数$f(x)=\left\{\begin{array}{l}1,x>0\\-1,x<0\end{array}\right.$,设$g(x)=\frac{f(x)}{x^2}$,则g(x)是( )
| A. | 奇函数,在(-∞,0)上递增,在(0,+∞)上递增 | |
| B. | 奇函数,在(-∞,0)上递减,在(0,+∞)上递减 | |
| C. | 偶函数,在(-∞,0)上递增,在(0,+∞)上递增 | |
| D. | 偶函数,在(-∞,0)上递减,在(0,+∞)上递减 |
8.已知集合A={x|0≤x≤5},B={x∈N*|x-1≤2},则A∩B=( )
| A. | {x|0≤x≤3} | B. | {1,2,3} | C. | {0,1,2,3} | D. | {x|1≤x≤3} |
15.已知$\frac{1}{sinφ}$+$\frac{1}{cosφ}$=2$\sqrt{2}$,若φ∈(0,$\frac{π}{2}$),则${∫}_{-1}^{tanφ}$(x2-2x)dx=( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
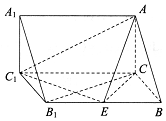 如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.
如图所示,在三棱柱ABC-A1B1C1中,已知AC⊥平面BCC1B1,AC=BC=1,BB1=2,∠B1BC=60°.