题目内容
(1)已知0<x<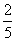
，求y＝2x－5x2的最大值；
(2)求函数y＝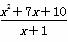
(x>－1)的最小值．
解 (1)y＝2x－5x2＝x(2－5x)＝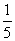
·5x·(2－5x)．
∵0<x<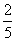，∴5x<2,2－5x>0，
∴5x(2－5x)≤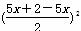
＝1，
∴y≤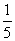，当且仅当5x＝2－5x，即x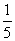＝时，ymax＝.
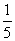(2)设x＋1＝t，则x＝t－1(t>0)，
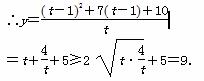当且仅当t＝
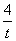，即t＝2，且此时x＝1时，取等号，
∴ymin＝9.
练习册系列答案
黄冈冠军课课练系列答案
长江作业本同步练习册系列答案
相关题目
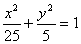与曲线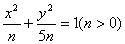
有相同的（ ）
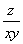取得最小值时，x＋2y－z的最大值为________．
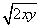≤λ(x＋y)恒成立，则实数λ的最小值为________．
，若函数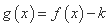
有两个不同的零点，
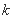的取值范围是 .
”是“
”的（ ）