题目内容
1.已知定义在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{log_2}(x+1),{\;}_{\;}x∈[0,1]\\|x-3|-1,{\;}_{\;}x∈(1,+∞)\end{array}$,则关于x的方程f(x)=a,(0<a<1)的所有根之和为( )| A. | 2a-1 | B. | 2a+1 | C. | 1-2-a | D. | 1+2-a |
分析 根据已知画出函数f(x)的图象,根据函数的对称性,结合指数和对数的运算性质,可得答案.
解答 解:∵函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=$\left\{\begin{array}{l}{log_2}(x+1),{\;}_{\;}x∈[0,1]\\|x-3|-1,{\;}_{\;}x∈(1,+∞)\end{array}$,
故函数f(x)的图象如下图所示: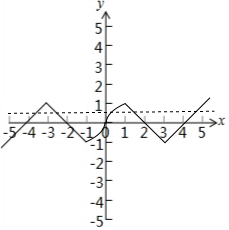
故关于x的方程f(x)=a,(0<a<1)共有5个根:x1,x2,x3,x4,x5,
则x1+x2+x4+x5=0,x1+x2+x3+x4+x5=x3,
由log2(x3+1)=a得:x3=2a-1,
故关于x的方程f(x)=a,(0<a<1)的所有根之和为2a-1,
故选:A.
点评 本题考查的知识点是根的存在性及根的个数判断,函数的图象,数形结合思想,难度中档.

练习册系列答案
相关题目
6.设数列{an}满足a1=1,a2=4,a3=9,an=an-1+an-2-an-3,n=4,5,…,则a2017=( )
| A. | 8064 | B. | 8065 | C. | 8067 | D. | 8068 |