题目内容
 如图,已知点B在以AC为直径的圆上,SA⊥面ABC,AE⊥SB于E,AF⊥SC于F.
如图,已知点B在以AC为直径的圆上,SA⊥面ABC,AE⊥SB于E,AF⊥SC于F.(Ⅰ)证明:SC⊥EF;
(Ⅱ)若SA=a,∠ASC=45°,∠AFE=30°,求三棱锥S-AEF的体积.
考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:(I)由SA⊥BC,得BC⊥面SAB,从而BC⊥AE.由AE⊥SB,BC⊥AE,得AE⊥面SBC,由此能证明SC⊥EF.
(Ⅱ)由已知得AF=SF=
a,AE⊥面SBC,由此能求出三棱锥S-AEF的体积.
(Ⅱ)由已知得AF=SF=
| ||
| 2 |
解答:
(I)解:∵SA⊥面ABC,∴SA⊥BC,
∵B在以AC为直径的圆上,
∴BC⊥面SAB,又AE?平面SAB,
∴BC⊥AE.
∵AE⊥SB,BC⊥AE,SB∩BC=B,
∴AE⊥面SBC,又SC?面SBC,
∴AE⊥SC.
∵AE⊥SC,AF⊥SC,AE∩AF=A,
∴SC⊥平面AEF,又EF?平面AEF,
∴SC⊥EF.
(Ⅱ)Rt△SAC中,∵SA=a,∠ASC=450∴AC=a,SC=
a,
又AF⊥SC,∴F为SC的中点,∴AF=SF=
a,
由(I)知AE⊥面SBC,
∴在Rt△AEF中,由AF=
a,∠AFE=300
得AE=
a,EF=
a,
∴S△AEF=
×
a×
a=
a2,
由(I)知SC⊥面AEF,∴VS-AEF=
×
a2×
a=
a3.
∵B在以AC为直径的圆上,
∴BC⊥面SAB,又AE?平面SAB,
∴BC⊥AE.
∵AE⊥SB,BC⊥AE,SB∩BC=B,
∴AE⊥面SBC,又SC?面SBC,
∴AE⊥SC.
∵AE⊥SC,AF⊥SC,AE∩AF=A,
∴SC⊥平面AEF,又EF?平面AEF,
∴SC⊥EF.
(Ⅱ)Rt△SAC中,∵SA=a,∠ASC=450∴AC=a,SC=
| 2 |
又AF⊥SC,∴F为SC的中点,∴AF=SF=
| ||
| 2 |
由(I)知AE⊥面SBC,
∴在Rt△AEF中,由AF=
| ||
| 2 |
得AE=
| ||
| 4 |
| ||
| 4 |
∴S△AEF=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
| ||
| 16 |
由(I)知SC⊥面AEF,∴VS-AEF=
| 1 |
| 3 |
| ||
| 16 |
| ||
| 2 |
| ||
| 96 |
点评:本题考查异面直线垂直的证明,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
设f(x)是定义在实数集R上的奇函数,且满足f(x+2)=-f(x),当0≤x≤1时,有f(x)=x,则f(7.5)=( )
| A、7.5 | B、1.5 |
| C、0.5 | D、-0.5 |
 如图,四边形ABCD内接于⊙O,边AD,BC的延长线交于点P,直线AE切⊙O于点A,且AB•CD=AD•PC.求证:
如图,四边形ABCD内接于⊙O,边AD,BC的延长线交于点P,直线AE切⊙O于点A,且AB•CD=AD•PC.求证: 为了绿化城市,准备在如图所示的区域DFEBC内修建一个矩形PQRC的草坪,并建立如图平面直角坐标系,且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用,经测量AB=100m,BC=80m,AE=30m,AF=20m.
为了绿化城市,准备在如图所示的区域DFEBC内修建一个矩形PQRC的草坪,并建立如图平面直角坐标系,且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用,经测量AB=100m,BC=80m,AE=30m,AF=20m.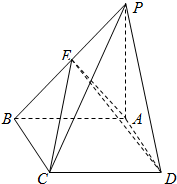 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,且PA=AB=1,F为PB中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,且PA=AB=1,F为PB中点. 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=