题目内容
数列{an}首项a1=1,前n项和Sn与an之间满足an=
(n≥2)
(1)求证:数列{
}是等差数列
(2)求数列{an}的通项公式.
| 2Sn2 |
| 2Sn-1 |
(1)求证:数列{
| 1 |
| Sn |
(2)求数列{an}的通项公式.
考点:数列递推式,等差关系的确定
专题:等差数列与等比数列
分析:(1)根据等差数列的定义,将条件求an=
(n≥2)进行转化即可证明数列{
}是等差数列
(2)根据{
}是等差数列 即可求数列{an}的通项公式.
| 2Sn2 |
| 2Sn-1 |
| 1 |
| Sn |
(2)根据{
| 1 |
| Sn |
解答:
解:(1)∵当n≥2时,an=Sn-Sn-1=
,
整理得:Sn-1-Sn=2Sn?Sn-1,
由题意知Sn≠0,
∴
-
=2,
即{
}是以
=
=1为首项,公差d=2的等差数列.
(2)∵{
}是以
=
=1为首项,公差d=2的等差数列.
∴
=1+2(n-1)=2n-1,
∴Sn=
,n∈N•.,
当n≥2时,an=Sn-Sn-1=
-
=-
,
当n=1时,a1=S1=1不满足an,
∴an=
.
2
| ||
| 2Sn-1 |
整理得:Sn-1-Sn=2Sn?Sn-1,
由题意知Sn≠0,
∴
| 1 |
| Sn |
| 1 |
| Sn-1 |
即{
| 1 |
| Sn |
| 1 |
| S1 |
| 1 |
| a1 |
(2)∵{
| 1 |
| Sn |
| 1 |
| S1 |
| 1 |
| a1 |
∴
| 1 |
| Sn |
∴Sn=
| 1 |
| 2n-1 |
当n≥2时,an=Sn-Sn-1=
| 1 |
| 2n-1 |
| 1 |
| 2(n-1)-1 |
| 2 |
| (2n-1)(2n-3) |
当n=1时,a1=S1=1不满足an,
∴an=
|
点评:本题主要考查等差数列的通项公式和等差数判断,要求熟练掌握等差数列的通项公式,考查学生的计算能力.

练习册系列答案
相关题目
设f(x)=ex+x-4,则函数f(x)=0的解位于区间( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
极坐标方程ρcosθ=4表示的曲线是( )
| A、一条平行于极轴的直线 |
| B、一条垂直于极轴的直线 |
| C、圆心在极轴上的圆 |
| D、过极点的圆 |
已知全集为R,集合A={x|
≤1},B={x|-1≤x≤3},则A∩∁RB=( )
| 1 |
| x |
| A、(-1,3) |
| B、[-1,0]∪[1,3] |
| C、(-∞,-1)∪(3,+∞) |
| D、[1,3] |
已知集合M={x|
≥0,x∈R},集合N={x||x|≤1,x∈R},则M∩N=( )
| x |
| x+1 |
| A、{x|0<x≤1} |
| B、{x|0≤x≤1} |
| C、{x1-1<x≤1} |
| D、{x1-1<x≤1} |
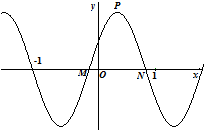 已知函数
已知函数