题目内容
在数列{an}中,若a1=2,a2=6,且当n∈N*时,an+2是an•an+1的个位数字,则a2014等于( )
| A、2 | B、4 | C、6 | D、8 |
考点:归纳推理
专题:归纳法
分析:通过计算:a3,a4,a5,a6,a7,a8,….由以上观察到:an+6=an.即可得出.
解答:
解:①∵a1a2=2×6=12,其个位数是2,∴a3=2;
②∵a2a3=2×6=12,其个位数是2,∴a4=2;
③∵a3a4=2×2=4,其个位数是4,∴a5=4;
④∵a4a5=2×4=8,其个位数是8,∴a6=8;
⑤∵a5a6=4×8=32,其个位数是2,∴a7=2;
⑥∵a6a7=2×8=16,其个位数是6,∴a8=6;
….
由以上观察到:an+6=an.
∴a2014=a6×335+4=a4=2.
∴a2014=2.
故选:A.
②∵a2a3=2×6=12,其个位数是2,∴a4=2;
③∵a3a4=2×2=4,其个位数是4,∴a5=4;
④∵a4a5=2×4=8,其个位数是8,∴a6=8;
⑤∵a5a6=4×8=32,其个位数是2,∴a7=2;
⑥∵a6a7=2×8=16,其个位数是6,∴a8=6;
….
由以上观察到:an+6=an.
∴a2014=a6×335+4=a4=2.
∴a2014=2.
故选:A.
点评:本题考查了利用“归纳法”求数列的通项公式,考查了推理能力,属于基础题.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
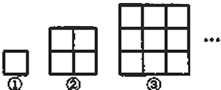 如图图形都是由同样大小的正方形按一定规律组成,第①个图形中有1个正方形,第②个图形中有5个正方形,…,则第⑥个图形中正方形的个数是( )
如图图形都是由同样大小的正方形按一定规律组成,第①个图形中有1个正方形,第②个图形中有5个正方形,…,则第⑥个图形中正方形的个数是( )| A、36 | B、55 | C、70 | D、91 |
顶点在原点,起始边与x轴正半轴重合,且和α=
终边相同的角可以是( )
| π |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、
|
平面α的一个法向量
=(1,-1,0),则y轴与平面α所成的角的大小为( )
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
设α,β为两个不重合的平面,m,n是两条不重合的直线,则下列四个命题中是真命题的是( )
| A、若m⊥n,m⊥α,则n∥α |
| B、若n?α,m?β,α与β相交且不垂直,则n与m不垂直 |
| C、若α⊥β,α∩β=m,m⊥n,则n⊥β |
| D、若m∥n,n⊥α,α∥β,则m⊥β |