题目内容
已知两条不同直线l，m以及△ABC，直线l⊥AB，l⊥AC，直线m⊥BC，m⊥AC，则直线l，m的位置关系是（ ）
| A、相交 | B、平行 |
| C、异面 | D、以上都有可能 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：由直线垂直于平面的判定定理知l，m都垂直于平面ABC，再由直线垂直于平面的性质定理进行判断．
解答：
解：∵直线l⊥AB，l⊥AC，AB∩AC=A，
∴l⊥平面ABC，
∵直线m⊥BC，m⊥AC，BC∩AC=C，
∴m⊥平面ABC，
∴l∥m．
故选B．
∴l⊥平面ABC，
∵直线m⊥BC，m⊥AC，BC∩AC=C，
∴m⊥平面ABC，
∴l∥m．
故选B．
点评：本题考查空间中直线与直线的位置关系，是基础题，解题时要直线垂直于平面的判定定理和性质定理的灵活运用．
练习册系列答案
相关题目
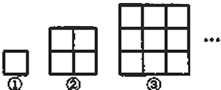如图图形都是由同样大小的正方形按一定规律组成，第①个图形中有1个正方形，第②个图形中有5个正方形，…，则第⑥个图形中正方形的个数是（ ）| A、36 | B、55 | C、70 | D、91 |
顶点在原点，起始边与x轴正半轴重合，且和α=
终边相同的角可以是（ ）
| π |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、
|
有一个几何体的三视图如图所示，这个几何体是一个（ ）
| A、棱台 | B、棱锥 | C、棱柱 | D、圆台 |
平面α的一个法向量
=（1，-1，0），则y轴与平面α所成的角的大小为（ ）
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
在空间内，设l，m，n是三条不同的直线，α，β，γ是三个不同的平面，则下列命题中为假命题的是（ ）
| A、α⊥γ，β⊥γ，α∩β=l，则l⊥γ |
| B、l∥α，l∥β，α∩β=m，则l∥m |
| C、α∩β=l，β∩γ=m，γ∩α=n，l∥m，则l∥n |
| D、α⊥γ，β⊥γ，则α⊥β或α∥β |
函数y=sin2x-3cosx+2的最小值为（ ）
| A、5 | B、0 | C、2 | D、-1 |