题目内容
13.已知在直角梯形ABCD中,∠ADC=∠DAB=90°,△ADC与△ABC均为等腰直角三角形,且AD=1,将直角梯形ABCD沿AC折叠成三棱锥D-ABC,当三棱锥D-ABC的体积取得最大值时,其外接球的表面积为4π.分析 画出图形,确定三棱锥外接球的半径,然后求解外接球的表面积即可.
解答 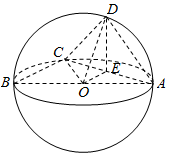 解:如图:AB=2,AD=1,CD=1,
解:如图:AB=2,AD=1,CD=1,
∴AC=$\sqrt{2}$,BC=$\sqrt{2}$,
取AC的中点E,AB的中点O,连结DE,OE,
当三棱锥体积最大时,平面DCA⊥平面ACB,
∵DE⊥AC,
∴DE⊥平面ACB,
∵DE=$\frac{\sqrt{2}}{2}$,OE=$\frac{\sqrt{2}}{2}$,
∴OD=1,
∴OB=OA=OC=OD,
∴OB=1,就是外接球的半径为1,
此时三棱锥外接球的表面积为4π•12=4π.
故答案为:4π.
点评 本题考查折叠问题,三棱锥的外接球的表面积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
7.已知双曲线$\frac{{x}^{2}}{3}$-y2=1,过右焦点向其渐近线作垂线,与两条渐近线分别交于A,B两点,O为坐标原点,则三角形AOB的面积是( )
| A. | $\frac{3}{2}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
 ,其前
,其前 项和为
项和为 ,若
,若 ,
, ,则数列
,则数列 .
.