题目内容
1.在△ABC中,若a=1,b=$\sqrt{3}$,A+C=2B,则A=$\frac{π}{6}$.分析 利用三角形内角和定理求得B=$\frac{π}{3}$,由正弦定理,即可求得sinA,求得A.
解答 解:由三角形内角和定理可知,A+B+C=π,
∴B=$\frac{π}{3}$,
由正弦定理可知:$\frac{a}{sinA}=\frac{b}{sinB}$,
sinA=$\frac{asinB}{b}$=$\frac{1}{2}$,
A+C=2B,
∴A=$\frac{π}{6}$
故答案为:$\frac{π}{6}$.
点评 本题考查三角形内角和定理及正弦定理,要求学生熟练掌握正弦定理,属于基础题.

练习册系列答案
相关题目
13.函数f(x)=$\frac{1}{3}$x3-ax2-3a2x-4在(3,+∞)上是增函数,则实数a的取值范围是( )
| A. | a≥0 | B. | a≥1 | C. | a≤-3或a≥1 | D. | -3≤a≤1 |
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,P是直线x=a上一点,且PF1⊥PF2,|PF1|+|PF2|=2$\sqrt{2}$a,则双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2 | D. | $\sqrt{3}$ |
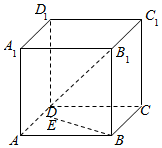 如图,已知正方体ABCD-A1B1C1D1中,E是平面ABCD上一动点,则直线BE与直线B1D所成角的余弦值的取值范围是[0,$\frac{\sqrt{6}}{3}$].
如图,已知正方体ABCD-A1B1C1D1中,E是平面ABCD上一动点,则直线BE与直线B1D所成角的余弦值的取值范围是[0,$\frac{\sqrt{6}}{3}$]. 不经过第一象限,则
不经过第一象限,则 的符号是( )
的符号是( ) B.
B. C.
C. D.
D.