题目内容
15.在△ABC中,已知AB=6,BC=4,AC=2$\sqrt{19}$,则tanB=$-\sqrt{3}$.分析 利用余弦定理求出B的余弦函数值,然后求解tanB.
解答 解:在△ABC中,已知AB=6,BC=4,AC=2$\sqrt{19}$,
可得cosB=$\frac{{AB}^{2}+{AC}^{2}-{BC}^{2}}{2AB•AC}$=$\frac{36+16-4×19}{2×6×4}$=$-\frac{1}{2}$.
B=120°.
tanB=$-\sqrt{3}$.
故答案为:-$\sqrt{3}$.
点评 本题考查余弦定理的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知函数f(x)=cos2x+2sinxcosx,则下列说法正确的是( )
| A. | f(x)的图象关于直线$x=\frac{5}{8}π$对称 | |
| B. | f(x)的图象关于点($-\frac{3}{8}π$,0)对称 | |
| C. | 若f(x1)=f(x2),则x1-x2=kπ,k∈Z | |
| D. | f(x)的图象向右平移$\frac{π}{4}$个单位长度后得$g(x)=\sqrt{2}sin(2x+\frac{π}{4})$ |
10.关于x的不等式0.23-2x<125的解集为( )
| A. | $\left\{{x\left|{x<\frac{1}{2}}\right.}\right\}$ | B. | $\left\{{x\left|{x>\frac{1}{2}}\right.}\right\}$ | C. | {x|x≥-1} | D. | {x|x<3} |
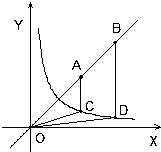 如图,点A、B为直线y=x上的两点,过A、B两点分别作y 轴的平行线交双曲线y=$\frac{1}{x}$(x>0)于C、D两点.若BD=2AC,则4OC2-OD2的值为6.
如图,点A、B为直线y=x上的两点,过A、B两点分别作y 轴的平行线交双曲线y=$\frac{1}{x}$(x>0)于C、D两点.若BD=2AC,则4OC2-OD2的值为6.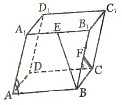 已知平行六面体ABCD-A1B1C1D1的所有棱长都是1,且∠A1AB=∠A1AD=∠BAD=60°,E、F分别为A1B1与BB1的中点,求异面直线BE与CF所成的角.
已知平行六面体ABCD-A1B1C1D1的所有棱长都是1,且∠A1AB=∠A1AD=∠BAD=60°,E、F分别为A1B1与BB1的中点,求异面直线BE与CF所成的角.