Question

4．已知SA垂直正方形ABCD所在的平面，过A作-个平面AEF垂直SC，平面AEF分别交SB、SD于E、F．求证AF垂直SD．

Answer 1

分析 证明AF⊥CD，AF⊥SC，可得AF⊥平面SCD，即可证明AF垂直SD．

解答 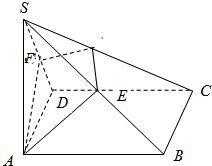证明：∵SA垂直正方形ABCD所在的平面，SA?平面SAD，
∴平面SAD⊥平面ABCD，
∵CD⊥AD，
∴CD⊥平面SAD，
∵AF?平面SAD，
∴AF⊥CD，
∵过A作-个平面AEF垂直SC，平面AEF分别交SB、SD于E、F，
∴AF⊥SC，
∵SC∩CD=C，
∴AF⊥平面SCD，
∵SD?平面SCD，
∴AF⊥SD．

点评 本题考查线面垂直的判定与性质，考查学生分析解决问题的能力，正确运用线面垂直的判定与性质是关键．