题目内容
14.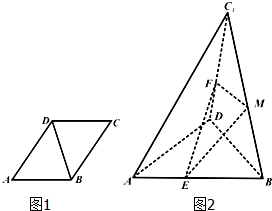 已知菱形ABCD中,AB=4,∠BAD=60°,将菱形ABCD沿对角线BD翻折,使点C翻折到点C1的位置,点E,F,M分别是AB,DC1,BC1的中点.
已知菱形ABCD中,AB=4,∠BAD=60°,将菱形ABCD沿对角线BD翻折,使点C翻折到点C1的位置,点E,F,M分别是AB,DC1,BC1的中点.(I)求证:AC1⊥BD;
(Ⅱ)当EM=$\sqrt{6}$时,求三棱锥B-EFM的体积.
分析 (I)根据菱形的对角线相互垂直,得到C1O⊥BD且AO⊥BD,所以BD⊥平面AOC1,从而得到平面AC1O内的直线AC1BD.
(Ⅱ)求出E到平面BFM的距离,利用VB-EFM=VE-BMF,结合体积公式,即可求三棱锥B-EFM的体积.
解答 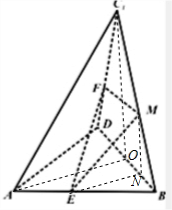 (I)证明:在菱形ABCD中,设O为AC,BD的交点,则AC⊥BD.
(I)证明:在菱形ABCD中,设O为AC,BD的交点,则AC⊥BD.
连接AO,C1O
∴在三棱锥C1-ABD中,C1O⊥BD,AO⊥BD.
又 C1O∩AO=O,
∴BD⊥平面AOC1.
又∵AC1?平面AOC1,
∴BD⊥AC1.
(Ⅱ)解:取OB的中点N,连接MN,EN,则EN=MN=$\sqrt{3}$,
∵EM=$\sqrt{6}$,
∴∠MNE=90°,
∴E到平面BFM的距离为ENsin90°=$\sqrt{3}$
∴VB-EFM=VE-BMF=$\frac{1}{3}×\frac{1}{2}×2×\sqrt{3}×\sqrt{3}×\sqrt{3}$=$\sqrt{3}$.
点评 本题根据一个平面图形的翻折,求证线线垂直,求三棱锥B-EFM的体积.着重考查线面垂直的判定与性质和锥体体积公式等知识,属于中档题.

练习册系列答案
相关题目
9.在数列{an}中,a1=-1,an+1=an-3,则a4=( )
| A. | -10 | B. | -7 | C. | -5 | D. | 11 |
19.函数f(x)=x-2lnx在区间[1,e]上的最小值和最大值分别是( )
| A. | 1和e-2 | B. | 2-2ln2和e-2 | C. | -1和e-2 | D. | 2-2ln2和1 |