题目内容

9．在数列{an}中，a1=-1，an+1=an-3，则a4=（　　）
A．-10B．-7C．-5D．11

分析 由题意易得数列{an}是-1为首项-3为公差的等差数列，由通项公式可得．

解答 解：∵在数列{an}中，a1=-1，an+1=an-3，
∴an+1-an=-3，即数列{an}是-1为首项-3为公差的等差数列，
∴a4=-1+3×（-3）=-10，
故选：A．

点评 本题考查等差数列的通项公式，属基础题．

练习册系列答案
相关题目
19．已知等差数列{an}满足a3+a4=12，3a2=a5，则a5=（　　）
A．3B．6C．9D．11
20．设集合A={1，2，3，4，5}，B={2，4，5，7，8}，则A∩B={2，4，5}．
17．某校高一、高二和高三年级分别有学生1000名、800名和700名，现用分层抽样的方法从中抽取容量为100的样本，则抽出的高二年级的学生人数为32．
4．已知$\overrightarrow a，\overrightarrow b，\overrightarrow c$在同一平面内，且$\overrightarrow a=（-1，2）$．
（1）若$\overrightarrow c=（m-1，3m）$，且$\overrightarrow c∥\overrightarrow a$，求m的值；
（2）若|$\overrightarrow a-\overrightarrow b|=3$，且$（\overrightarrow a+2\overrightarrow b）⊥（2\overrightarrow a-\overrightarrow b）$，求向量$\overrightarrow a-\overrightarrow b$与$\overrightarrow b$的夹角．
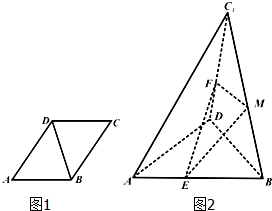14．已知菱形ABCD中，AB=4，∠BAD=60°，将菱形ABCD沿对角线BD翻折，使点C翻折到点C1的位置，点E，F，M分别是AB，DC1，BC1的中点．
（I）求证：AC1⊥BD；
（Ⅱ）当EM=$\sqrt{6}$时，求三棱锥B-EFM的体积．
1．某次考试的第一大题是由10个判断题组成，每个判断题做对得2分，不做或做错得0分．小明做对每一题的概率为$\frac{3}{4}$，则小明第一大题得分的方差是$\frac{15}{8}$．
18．对于数列{an}，定义数列{an+1-an}的数列{an}的“差数列”，若a1=2，{an}的“差数列”的通项公式为2n．
（1）求数列{an}的通项公式；
（2）设数列{an}的前n项和为Sn，求S1+2S2+…+nSn．
19．已知a＞$\frac{1}{2}$，且a≠1，条件p：函数f（x）=log（2a-1）x在其定义域上是减函数；
条件q：函数g（x）=$\sqrt{x+|x-a|-2}$的定义域为R，如果“p或q”为真，试求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网