题目内容
6.已知实数x,y满足$\left\{\begin{array}{l}x+y-2≥0\\ 2x-y-4≤0\\ x-2y+1≥0\end{array}\right.$,则目标函数z=2x+y的最大值是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 画出约束条件表示的可行域,判断目标函数z=2x+y的位置,求出最大值.
解答  解:作出约束条件$\left\{\begin{array}{l}x+y-2≥0\\ 2x-y-4≤0\\ x-2y+1≥0\end{array}\right.$的可行域如图:
解:作出约束条件$\left\{\begin{array}{l}x+y-2≥0\\ 2x-y-4≤0\\ x-2y+1≥0\end{array}\right.$的可行域如图:
目标函数z=2x+y在$\left\{\begin{array}{l}{x-2y+1=0}\\{2x-y-4=0}\end{array}\right.$的交点A(3,2)处取最大值为z=2×3+1×2=8.
故选:C.
点评 本题考查简单的线性规划的应用,正确画出可行域,判断目标函数经过的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知函数f(x)的定义域为R,对任意x1<x2,有f(x1)-f(x2)<x1-x2,且f(-3)=-4,则不等式f(log${\;}_{\frac{1}{2}}$|3x-1|)>log${\;}_{\frac{1}{2}}$|3x-1|-1的解集为( )
| A. | (2,+∞) | B. | (-∞,2) | C. | (0,1)∪(1,2) | D. | (-∞,0)∪(0,2) |
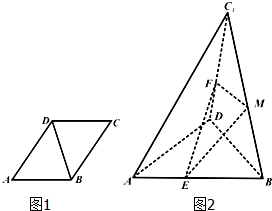 已知菱形ABCD中,AB=4,∠BAD=60°,将菱形ABCD沿对角线BD翻折,使点C翻折到点C1的位置,点E,F,M分别是AB,DC1,BC1的中点.
已知菱形ABCD中,AB=4,∠BAD=60°,将菱形ABCD沿对角线BD翻折,使点C翻折到点C1的位置,点E,F,M分别是AB,DC1,BC1的中点.