题目内容
14.如果$\frac{2π}{3}$弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( )| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{{4\sqrt{3}}}{9}π$ | D. | $\frac{{4\sqrt{3}}}{9}$ |
分析 由题意画出图形,解直角三角形求出扇形的半径,代入弧长公式求得答案.
解答 解:如图,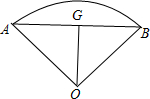
$∠AOB=\frac{2π}{3}$,AB=2,
过O作OG⊥AB于G,则AG=1,$∠AOG=\frac{π}{3}$,
∴sin$\frac{π}{3}=\frac{AG}{AO}$,即$AO=\frac{AG}{sin\frac{π}{3}}=\frac{1}{\frac{\sqrt{3}}{2}}=\frac{2\sqrt{3}}{3}$,
∴$\widehat{AB}=\frac{2\sqrt{3}}{3}×\frac{2π}{3}=\frac{4\sqrt{3}}{9}π$.
故选:C.
点评 本题考查弧长公式的应用,考查直角三角形中的边角关系,是基础的计算题.

练习册系列答案
相关题目
3.已知复数z=1+i(i是虚数单位),则$\frac{4-2i}{z}$的共轭复数是( )
| A. | -1+3i | B. | 1+3i | C. | 1-3i | D. | -1-3i |