题目内容
9.已知函数f(x)=x-4+$\frac{9}{x+1}$,x∈(0,4),当x=a时,f(x)取得最小值b,则函数g(x)=($\frac{1}{a}$)|x+b|的图象为( )| A. | 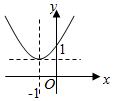 | B. | 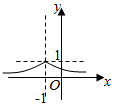 | C. | 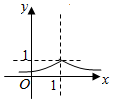 | D. |  |
分析 变形利用基本不等式即可得出a=2,b=1,利用函数g(x)=($\frac{1}{a}$)|x+b|为函数g(x)=($\frac{1}{2}$)|x+1|,关于直线x=-1对称,即可得出结论.
解答 解:∵x∈(0,4),∴x+1>1.
∴f(x)=x-4+$\frac{9}{x+1}$=x+1+$\frac{9}{x+1}$-5≥2$\sqrt{(x+1)•\frac{9}{x+1}}$-5=1,
当且仅当x=2时取等号,f(x)的最小值为1.
∴a=2,b=1,
∴函数g(x)=($\frac{1}{a}$)|x+b|为函数g(x)=($\frac{1}{2}$)|x+1|,关于直线x=-1对称.
故选:B.
点评 本题考查了变形利用基本不等式,考查数形结合的数学思想,属于中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
14.如果$\frac{2π}{3}$弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{{4\sqrt{3}}}{9}π$ | D. | $\frac{{4\sqrt{3}}}{9}$ |
1.下列命题的说法错误的是( )
| A. | 若p∧q为假命题,则p,q均为假命题 | |
| B. | 命题“?x∈R,x2+x+1>0”为真命题. | |
| C. | “x=-1”是“x2-3x+2>0”的充分不必要条件 | |
| D. | 命题“若x2-3x+2=0,则 x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
18.正数a,b满足a-2ab+b=0,则2a+b的最小值为( )
| A. | $\frac{3}{2}+\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $1+\sqrt{2}$ | D. | 3 |