题目内容
已知直线l的极坐标方程为ρsinθ=2,曲线C的参数方程为
(t为参数),则l与C交点的一个极坐标为 .
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:首先,将给定的直线的极坐标方程化为直角坐标方程,然后,将曲线的参数方程化为普通方程,联立方程组求解交点坐标,然后,写出其极坐标形式即可.
解答:
解:由直线l的极坐标方程为ρsinθ=2,得
y=2,
曲线C的参数方程为
(t为参数),得
y2-x2=4,
联立
,得
,故交点坐标为(0,2),
它的极坐标方程为(2,
),
故答案为:(2,
).
y=2,
曲线C的参数方程为
|
y2-x2=4,
联立
|
|
它的极坐标方程为(2,
| π |
| 2 |
故答案为:(2,
| π |
| 2 |
点评:本题重点考查了直线的极坐标方程、双曲线的参数方程等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠A=30°,a=b=1,则S△ABC=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,EA与圆O相切于点A,D是EA的中点,过点D引圆O的割线,与圆O相交于点B,C,连结EC.
如图,EA与圆O相切于点A,D是EA的中点,过点D引圆O的割线,与圆O相交于点B,C,连结EC.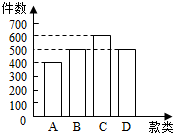 随着社会的发展,网上购物已成为一种新型的购物方式,某商家在网上新推出A,B,C,D四款商品,进行限时促销活动,规定每位注册会员限购一件,并需在网上完成对所购商品的质量评价,以下为四款商品销售情况的条形图和分层抽样法选取100份评价的统计表:
随着社会的发展,网上购物已成为一种新型的购物方式,某商家在网上新推出A,B,C,D四款商品,进行限时促销活动,规定每位注册会员限购一件,并需在网上完成对所购商品的质量评价,以下为四款商品销售情况的条形图和分层抽样法选取100份评价的统计表: