题目内容
函数f(x)＝ax3＋bx在x＝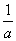
处有极值，则ab的值为( )
A．2 B．－2 C．3 D．－3
D
解析 f′(x)＝3ax2＋b，由f′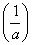
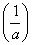＝3a2＋b＝0，可得ab＝－3.故选D.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
函数f(x)＝ax3＋bx在x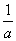＝处有极值，则ab的值为( )
A．2 B．－2 C．3 D．－3
D
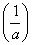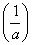解析 f′(x)＝3ax2＋b，由f′＝3a2＋b＝0，可得ab＝－3.故选D.
阅读快车系列答案
，曲线y＝f(x)在点(2，f(2))处的切线方程为7x－4y－12＝0.
(a>0)的单调递减区间是________．
m B.
m C.
m D.
m
＋cos α，且α∈
，则
的值为________．