题目内容
设椭圆C:
+
=1(a>b>0)过点(1,
),F1、F2分别为椭圆C的左、右两个焦点,且离心率e=
.
(1)求椭圆C的方程;
(2)已知O为坐标原点,直线l过椭圆的右焦点F2与椭圆C交于M、N两点.若OM、ON 的斜率k1,k2满足k1+k2=-3,求直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
(1)求椭圆C的方程;
(2)已知O为坐标原点,直线l过椭圆的右焦点F2与椭圆C交于M、N两点.若OM、ON 的斜率k1,k2满足k1+k2=-3,求直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由椭圆的离心率e=
,得椭圆方程为
+
=1,把点(1,
)代入,能求出椭圆的方程.
(2)设直线l为y=k(x-1),代入椭圆方程
+
=1,得(3+4k2)x2-8k2x+4k2-12=0,由此利用根的判别式、韦达定理,结合已知条件能求出直线MN的方程.
| 1 |
| 2 |
| x2 |
| 4c2 |
| y2 |
| 3c2 |
| 3 |
| 2 |
(2)设直线l为y=k(x-1),代入椭圆方程
| x2 |
| 4 |
| y2 |
| 3 |
解答:
解:(1)∵椭圆C:
+
=1(a>b>0)过点(1,
),
F1、F2分别为椭圆C的左、右两个焦点,且离心率e=
,
∴
=
,∴a=2c,∴b2=a2-c2=3c2,
∴椭圆方程为
+
=1.…(2分)
把点(1,
)代入椭圆,得
+
=1,解得c2=1.
∴椭圆的方程为
+
=1.…(4分)
(2)若直线l斜率不存在,k1 +k2=0不合题意,
∴直线l的斜率存在.…(5分)
设直线l为y=k(x-1),代入椭圆方程
+
=1,
得(3+4k2)x2-8k2x+4k2-12=0.…(7分)
依题意△=9k2+9>0.
设M(x1,y1),N(x2,y2),则x1+x2=
,x1x2=
.…(8分)
∵k1+k2=-3,
∴k1+k2=
+
=k(
+
)
=k(2-
)
=k(2-
)=-3.…(10分)
整理,得k2-2k-3=0,解得k=3或k=-1.
∴所求直线MN的方程为3x-y-3=0或x+y-1=0.…(12分)
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
F1、F2分别为椭圆C的左、右两个焦点,且离心率e=
| 1 |
| 2 |
∴
| c |
| a |
| 1 |
| 2 |
∴椭圆方程为
| x2 |
| 4c2 |
| y2 |
| 3c2 |
把点(1,
| 3 |
| 2 |
| 1 |
| 4c2 |
(
| ||
| 3c2 |
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)若直线l斜率不存在,k1 +k2=0不合题意,
∴直线l的斜率存在.…(5分)
设直线l为y=k(x-1),代入椭圆方程
| x2 |
| 4 |
| y2 |
| 3 |
得(3+4k2)x2-8k2x+4k2-12=0.…(7分)
依题意△=9k2+9>0.
设M(x1,y1),N(x2,y2),则x1+x2=
| 2k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
∵k1+k2=-3,
∴k1+k2=
| y1 |
| x1 |
| y2 |
| x2 |
| x1-1 |
| x1 |
| x2-1 |
| x2 |
=k(2-
| x1+x2 |
| x1x2 |
=k(2-
| 2k2 |
| k2-3 |
整理,得k2-2k-3=0,解得k=3或k=-1.
∴所求直线MN的方程为3x-y-3=0或x+y-1=0.…(12分)
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意韦达定理的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{an}对任意m,n∈N+都有am+n=am+an+3,若a1=3,则数列{an}的通项公式an=( )
| A、6n-3 | B、4n-1 |
| C、2n+1 | D、3n |
函数f(x)=
x2-lnx的单调递减区间为( )
| 1 |
| 2 |
| A、(-1,1) |
| B、(0,1] |
| C、[1,+∞) |
| D、(-∞,-1)∪(0,1] |
若抛物线y2=2px的焦点与椭圆
+
=1的右焦点重合,则p的值为( )
| x2 |
| 8 |
| y2 |
| 4 |
| A、-2 | B、2 | C、-4 | D、4 |
下面多面体中有12条棱的是( )
| A、四棱柱 | B、四棱锥 |
| C、五棱锥 | D、五棱柱 |
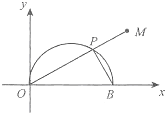 在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度.
在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度.